Latest micro-posts
You can also also view the full archives of micro-posts. Longer blog posts are available in the Articles section.
Lasagna were tasty last week!
“When the underlying measurements are normally distributed, you can “convert” a range measurement into an estimate for the standard deviation” using the D2 constant. As always, Rick Wicklin wrote a very interesting article for those involved in QC or dealing with small samples. See also On using flexible distributions to fit data for another interesting story.
Some estimators provide reasonable estimates even when there are correlations among observations, but estimates of uncertainties of estimates can be badly affected by correlations. — What Does a Statistical Method Assume?.
I have almost two years of backup data for my home directory, thanks to kopia. It works great, it runs smoothly and doesn’t harm the RAM or disk, and it wakes up nicely when the laptop returns from idle.
~/tmp
» kopia snapshot list
chl@aliquote:/home/chl
2022-10-31 21:00:37 CET k105eb1435351bfdfba85874cd06ebf75 14.9 GB drwxr-xr-x files:226411 dirs:45856 (monthly-18)
2022-11-30 22:00:39 CET k01dd605c67ca579cbec33fb5eb386648 15.5 GB drwxr-xr-x files:232391 dirs:46879 (monthly-17)
2022-12-31 23:00:38 CET k5a01672b76af59461061c3fe25003785 15.7 GB drwxr-xr-x files:234220 dirs:47516 (monthly-16,annual-3)
2023-01-31 21:00:13 CET kec7a24dd874b20376f160f1fe3e0acd8 15.4 GB drwxr-xr-x files:226071 dirs:45741 (monthly-15)
2023-02-28 21:00:08 CET kc707921ee53be6aa7ff2be4da99387c4 14.6 GB drwxr-xr-x files:228097 dirs:46041 (monthly-14)
--%<-----------------
2024-03-25 08:12:51 CET k9cb5afcc7ce355e2b64c8f980ef6bb24 14.1 GB drwxr-xr-x files:218701 dirs:35849 (hourly-11)
2024-03-25 09:00:14 CET kdec17d1a1ed35833b0eed730c491ed87 14.1 GB drwxr-xr-x files:218716 dirs:35849 (latest-10,hourly-10)
2024-03-25 10:00:35 CET ka52066cb5588c88a7d259140e5c02683 14.1 GB drwxr-xr-x files:218702 dirs:35849 (latest-9,hourly-9)
2024-03-25 11:00:35 CET kd96a4c841b76c75e4b5b569594f9e87b 14.1 GB drwxr-xr-x files:218704 dirs:35849 (latest-8,hourly-8)
2024-03-25 12:00:35 CET k0ec385fbd40ce68a14250da3e4e72ac9 14.1 GB drwxr-xr-x files:218710 dirs:35849 (latest-7,hourly-7)
2024-03-25 13:00:35 CET k635fb4cf4fd0e3f4c45c58b7a14ed690 14.1 GB drwxr-xr-x files:218730 dirs:35850 (latest-6,hourly-6)
2024-03-25 14:00:35 CET k722ecc32f98028829e258d2582548281 14.1 GB drwxr-xr-x files:218741 dirs:35851 (latest-5,hourly-5)
2024-03-25 15:00:35 CET k87f64132d71b14eccbc7f5bb362b53aa 14.1 GB drwxr-xr-x files:218732 dirs:35851 (latest-4,hourly-4)
2024-03-25 18:07:22 CET k4af30387d39daf1dd1b3002dffde3543 14.1 GB drwxr-xr-x files:218733 dirs:35851 (latest-3,hourly-3)
2024-03-25 19:00:35 CET k66f7a97a2b50611e047524da6cc0e640 14.1 GB drwxr-xr-x files:218745 dirs:35851 (latest-2,hourly-2)
2024-03-25 20:26:20 CET kbd44c2958916a894deab100da949f302 14.1 GB drwxr-xr-x files:218745 dirs:35851 (latest-1,hourly-1,daily-1,weekly-1,monthly-1,annual-1)
♪ Flock of Dimes · Given/Electric Life
Writing Python like it’s Rust. Or how to make use of Python types in a meaningful way.
♪ Passenger · Summer Rain
TIL about Faircamp which looks amazing.
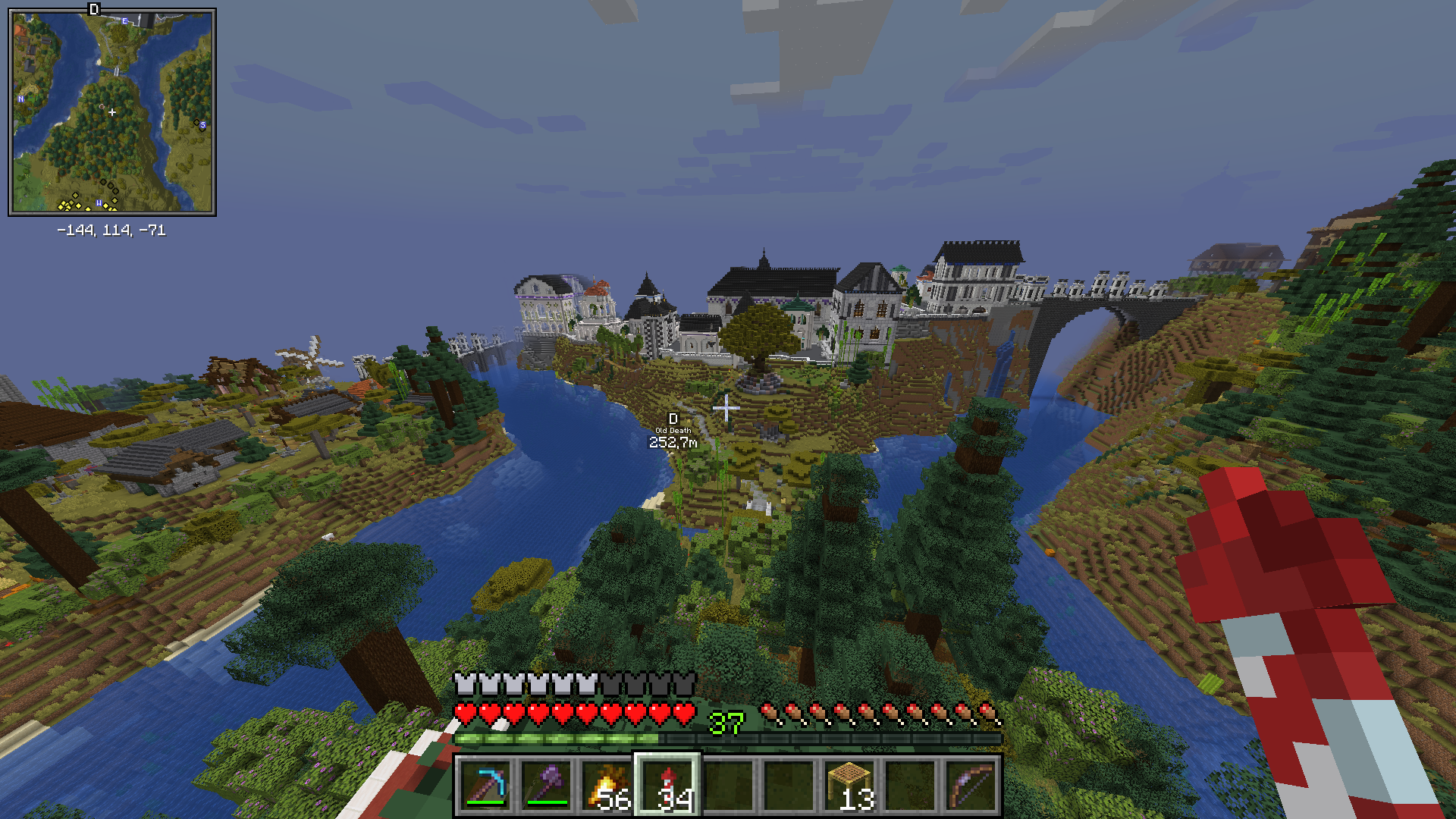
I recently switch from MC 1.19.4 with Forge and Optifine to MC 1.20.4 with Iris and Sodium. Now I got a lot more mods available with less frictions overall. And it looks like we can now play MC on a laptop with texture packs and shaders all time long.
It’s probably time to stop building on 1.19.4 I guess, and just start a new survival journey.