Armstrong numbers, named after Michael F. Armstrong, are numbers that are the sum of their own digits each raised to the power of the number of digits. For instance, 153 is an Armstrong number since 153 = 1³ + 5³ + 3³ = 1 + 125 + 27 = 153. They are also known as narcissistic numbers in number theory. What a funny name, isn’t it?

The following Racket program allows to test whether a given number, n, is an Armstrong number in base 10 or not:

#lang racket

(define (digits x)
  (if (zero? x)
      null
      (cons (remainder x 10)
            (digits (quotient x 10)))))

(define (armstrong-number? n)
  (let* ([d (digits n)]
         [l (length d)])
    (= n
       (for/sum ([a d])
         (expt a l)))))

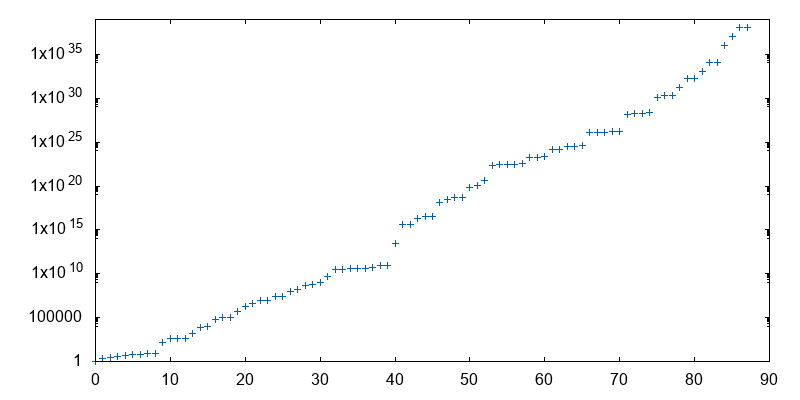
There are only 89 such numbers in base 10, and this is OEIS sequence A005188.

The above program works well for querying some numbers, but what if we want to generate the full sequence? The largest of these 89 numbers is: 115,132,219,018,763,992,565,095,597,973,971,522,401.

This is well above the limit of unsigned long long in C. So we will probably need the GMP library, and a more efficient screening algorithm. Here is one, from Rosetta. It runs in less than 15 s on my Macbook (1,3 GHz Intel Core m7), if we suppress the output: (source code)

~/tmp  cc armstrong-gmp.c -lgmp
~/tmp  time ./a.out > out
      14.44 real        13.97 user         0.12 sys
~/tmp  cat out | cut -d: -f 2 | gnuplot -p -e "set logscale y; plot '<cat'"

Thank God that number theory is unsullied by any application. — Leonard Dickson

I don’t know of any direct application of Armstrong numbers, even for recreational mathematics, but surely there are many other funny terms coined for interesting patterns, like amicable numbers, untouchable numbers, sociable numbers, abundant numbers, amenable numbers, or practical numbers.