lost+found 2014
Here are some draft notes, written in 2014, unfilled but not lost forever. With slight edits to accommodate a proper archive blog post.
Stata for structural equation modeling
(October 2014)
As Mplus syntax often appears a bit cryptic to carry out basic operations in Confirmatory Factor Analysis (CFA), I decided to write out some of the notes I took when using Mplus for recent psychometric studies.
In what follows, I will use data described and analyzed in Acock’s Stata textbook, Discovering Structural Equation Modeling Using Stata. Why this book? Essentially because it provides a ready-to-use dataset [describe it here], and the author discusses several applications of CFA models, including tests for measurement invariance, without much technical details. For those interested in a more rigorous approach, I can recommend Structural Equation Modeling. Applications Using Mplus, by Wang & Wang (2012, Wiley).
Multigroup analysis
In this post, I am interested in assessing weak and strong measurement invariance using Stata and Mplus. Both are popular statistical packages, and although these are commercial software they are worth their price, IMHO. Mplus includes more estimators than Stata, but probably we could tweak Stata commands to mimic Mplus.
A tutorial on multi-group CFAs with Stata can be found on the UCLA server: How can I check measurement invariance using the sem command?. Basically, measurement invariance can be assessed by fitting several nested models, where we impose additional constraints at each stage:
- (M1) all parameters free
- (M2) metric (pattern) invariance – loadings are invariant
- (M3) strong (scalar) invariance – loadings & intercepts are invariant
- (M4) strict invariance – loadings, intercepts & residuals are invariant
- (M5) strict invariance plus factor means are invariant
- (M6) strict invariance plus factor means & variances are invariant
Configural invariance is usually assessed using M1, the idea being to check that the hypothesized factor structure holds in all groups. It is also used as a reference (or baseline) model against which other models will be tested. Model M2 is the first step to demonstrate weak measurement invariance, that is M1 holds (i.e., factor loadings are as expected in all groups) but in addition loadings are equal in all subpopulations. We only allow item intercepts to differ between subgroups. Model M3 is used to test strong measurement invariance where in addition to loadings we impose that item intercepts are equal in all groups. A more constrained model, M4, also adds the constraint of equal errors of measurement. This model, and models M5-M6 are generally too strong, and hard to verify; after all, we only have one sample, and many researchers would be quite happy with demonstrating that strong measurement invariance is verified. [add reference]
To get the dataset under Stata, we write:
. use http://www.stata-press.com/data/dsemus/multgrp_cfa.dta
To create a standalone text file we will use the handy Stata program Stata2mplus, which allows to convert Stata data file to Mplus input file. This is easier than using Stata built-in converters since it will recode missing values, remove header, and select the correct field delimiter:
. stata2mplus using multgrp_cfa
This generates two files:
$ ls multgrp_cfa.*
multgrp_cfa.dat multgrp_cfa.inp
where the Mplus file contains details about items that were converted and basic syntax to read the dat file later:
Data:
File is multgrp_cfa.dat ;
Variable:
Names are
female x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13;
Missing are all (-9999) ;
Analysis:
Type = basic ;
The sample is composed of 8,984 respondents, with about 50% of men and women.
. tabulate female
female | Freq. Percent Cum.
------------|-----------------------------------
Man | 4,599 51.19 51.19
Woman | 4,385 48.81 100.00
------------|-----------------------------------
Total | 8,984 100.00
Basic item statistics are provided below, as mean ± SD and range, and values for Cronbach alpha (unstandardized since all responses are expressed on the same 4-point scale):
. summarize x1-x3 x4 x9 x10 x12
Variable | Obs Mean Std. Dev. Min Max
-------------|--------------------------------------------------------
x1 | 7351 3.24092 .6674483 1 4
x2 | 7474 2.188788 .6645846 1 4
x3 | 7375 3.659119 .5932246 1 4
x4 | 1833 2.331697 1.022223 1 4
x9 | 1811 2.276643 .9320571 1 4
-------------|--------------------------------------------------------
x10 | 1775 2.228732 1.072652 1 4
x12 | 1847 1.705468 .7425231 1 4
. alpha x1-x3 x4 x9 x10 x12, item
Test scale = mean(unstandardized items)
average
item-test item-rest interitem
Item | Obs Sign correlation correlation covariance alpha
-------------|-----------------------------------------------------------------
x1 | 7351 + 0.6973 0.3609 .1536247 0.6926
x2 | 7474 - 0.5810 0.3359 .1781062 0.7343
x3 | 7375 + 0.6428 0.3033 .1663125 0.6999
x4 | 1833 + 0.6226 0.3684 .1494082 0.7191
x9 | 1811 + 0.6401 0.4216 .147084 0.7077
x10 | 1775 + 0.6541 0.3978 .1432081 0.7101
x12 | 1847 + 0.6349 0.4660 .1504138 0.7027
-------------|-----------------------------------------------------------------
Test scale | .1541296 0.7398
-------------------------------------------------------------------------------
As can be seen, there are many missing data for items x4, x9, x10, and x12, which means that the sample size will be considerably reduced when using available data.
Fitting a baseline model
A model imposing equivalent form on all relationships between items and factors in men and women, but no equality constraints, can be fitted as follows:
. sem (Depress -> x1 x2 x3) (Gov_Resp -> x4 x9 x10 x12), group(female) ginvariant(none) means(Depress@0 Gov_Resp@0)
(7377 observations with missing values excluded)
Endogenous variables
Measurement: x1 x2 x3 x4 x9 x10 x12
Exogenous variables
Latent: Depress Gov_Resp
Fitting target model:
Iteration 0: log likelihood = -12363.307
Iteration 1: log likelihood = -12362.434
Iteration 2: log likelihood = -12362.43
Iteration 3: log likelihood = -12362.43
Structural equation model Number of obs = 1607
Grouping variable = female Number of groups = 2
Estimation method = ml
Log likelihood = -12362.43
( 1) [x1]0bn.female#c.Depress = 1
( 2) [x4]0bn.female#c.Gov_Resp = 1
( 3) [mean(Depress)]0bn.female = 0
( 4) [mean(Gov_Resp)]0bn.female = 0
( 5) [x1]1.female#c.Depress = 1
( 6) [x4]1.female#c.Gov_Resp = 1
( 7) [mean(Depress)]1.female = 0
( 8) [mean(Gov_Resp)]1.female = 0
---%<-------------------------------------------------------------------------
LR test of model vs. saturated: chi2(26) = 51.00, Prob > chi2 = 0.0024
. estat gof, stats(all)
----------------------------------------------------------------------------
Fit statistic | Value Description
---------------------|------------------------------------------------------
Likelihood ratio |
chi2_ms(26) | 50.999 model vs. saturated
p > chi2 | 0.002
chi2_bs(42) | 2312.800 baseline vs. saturated
p > chi2 | 0.000
---------------------|------------------------------------------------------
Population error |
RMSEA | 0.035 Root mean squared error of approximation
90% CI, lower bound | 0.020
upper bound | 0.049
---------------------|------------------------------------------------------
Information criteria |
AIC | 24812.859 Akaike's information criterion
BIC | 25049.673 Bayesian information criterion
---------------------|------------------------------------------------------
Baseline comparison |
CFI | 0.989 Comparative fit index
TLI | 0.982 Tucker-Lewis index
---------------------|------------------------------------------------------
Size of residuals |
SRMR | 0.030 Standardized root mean squared residual
CD | 0.945 Coefficient of determination
----------------------------------------------------------------------------
Note: pclose is not reported because of multiple groups.
The key options are group(female) ginvariant(none), which indicate that we want to consider a grouping factor but we do not want to add constraints on the measurement model in each group. Factor means are constrained to equal 0 in both groups, but not their variances.
With Mplus, we would use the following script. Note that Mplus does not use listwise deletion by default, so we have to specify this ‘non-feature’ using listwise is on; in order to ensure we are working with the same set of 1,607 subjects. With Mplus, factor means are written as is while factor variances are put into brackets. Constraints are represented by the symbol @. So [DEP@0] means that variance for factor Depression is constrained to be zero. For multi-group analysis, we need to add a GROUPING = option, and this will be used to formulate different factor structure (or constraints) in each group, as indicated by each MODEL: step.
Data:
File is multgrp_cfa.dat ;
LISTWISE is ON;
Variable:
NAMES = female x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13;
USEVARIABLES = x1-x3 x4 x9 x10 x12;
GROUPING = female (0=M 1=F);
MISSING are ALL (-9999) ;
MODEL:
DEP BY x1@1 x2-x3*;
GOV BY x4@1 x9* x10* x12*;
DEP*; GOV*; ! free factor variances
[DEP@0 GOV@0]; ! zero factor means
MODEL F:
DEP BY x1@1 x2-x3*;
GOV BY x4@1 x9* x10* x12*;
OUTPUT:
TECH1 TECH4;
Results are provided below. Unless we specify the type of estimator we want to use, Mplus will default to an ML estimator, as Stata did.
MODEL FIT INFORMATION
Number of Free Parameters 37
Loglikelihood
H0 Value -12386.664
H1 Value -12336.930
Information Criteria
Akaike (AIC) 24847.328
Bayesian (BIC) 25046.467
Sample-Size Adjusted BIC 24928.925
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 99.468
Degrees of Freedom 33
P-Value 0.0000
Chi-Square Contribution From Each Group
M 44.009
F 55.459
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.050
90 Percent C.I. 0.039 0.062
Probability RMSEA <= .05 0.476
CFI/TLI
CFI 0.971
TLI 0.963
Chi-Square Test of Model Fit for the Baseline Model
Value 2312.800
Degrees of Freedom 42
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.049
The chi-square test that is reported under the term ‘baseline vs. saturated’ (Χ2(42) = 2312.800, p < 0.001) corresponds to what Mplus call ‘Chi-Square Test of Model Fit for the Baseline Model’, whereas that headed ‘model vs. saturated’ (Χ2(26) = 50.999, p = 0.002) is called ‘Chi-Square Test of Model Fit’ in Mplus.
FIXME: explain why DF differ between the two software!
Testing for invariance of factor loadings
With Stata, we just add ginvariant(mcoef) to constrain factor loadings to be equal in both groups. Using Mplus, we will just remove everything under the MODEL F: part, meaning that factor loadings for women will no longer be estimated freely but constrained to be qual to those of men.
Here are Mplus results:
MODEL FIT INFORMATION
Number of Free Parameters 32
Loglikelihood
H0 Value -12389.320
H1 Value -12336.930
Information Criteria
Akaike (AIC) 24842.639
Bayesian (BIC) 25014.867
Sample-Size Adjusted BIC 24913.209
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 104.779
Degrees of Freedom 38
P-Value 0.0000
Chi-Square Contribution From Each Group
M 46.335
F 58.444
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.047
90 Percent C.I. 0.036 0.058
Probability RMSEA <= .05 0.675
CFI/TLI
CFI 0.971
TLI 0.967
Chi-Square Test of Model Fit for the Baseline Model
Value 2312.800
Degrees of Freedom 42
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.049
Bifactor models
Here are some notes on Bifactor models, and their use in psychological or medical research.
As illustrated in the following picture (taken from Reise et al., 2010; see full reference below), a bifactor model differs from a second-order factor model in that (1) factor (or primary units) are not correlated, (2) the relation between indicators or items and the general factor is direct, and not mediated by specific factors as in a second-order factor model. As such, the bifactor model may be seen as a measurement model, unlike the later.
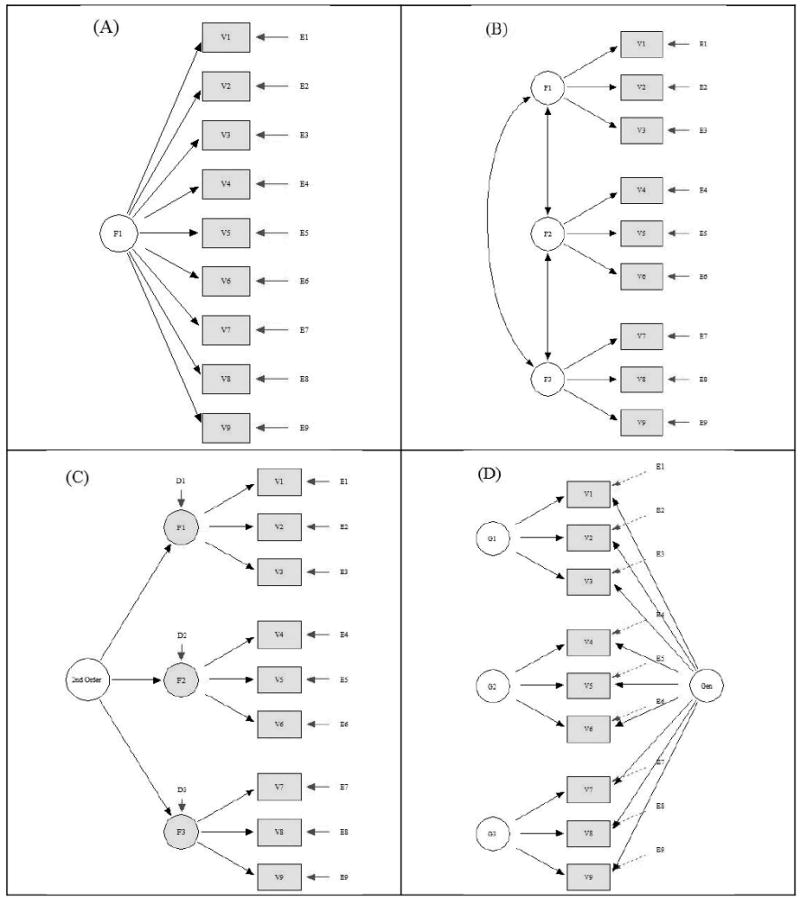
From Statalist, I found the following references on second-order factor and bifactor models (whenever possible I fixed dead links and tried to find ungated PDFs):
- Koufteros, X., Babbarb, S., & Kaighobadi, M. (2009). A paradigm for examining second-order factor models employing structural equation modeling. International Journal of Production Economics, 120(2), 633-652.
- Rindskopf, D., & Rose, T. (1988). Some theory and applications of confirmatory second-order factor analysis. Multivariate Behavioral Research, 23(1), 51-67.
- Chen, F.F., West, S.G., & Sousa, K.H. (2006). A Comparison of Bifactor and Second-Order Models of Quality of Life. Multivariate Behavioral Research, 41(2), 189–225.
- Chen, F.F., Hayes, A., Carver, C.S., Laurenceau, J.-P., Zhang, Z. (2012). Modeling General and Specific Variance in Multifaceted Constructs: A Comparison of the Bifactor Model to Other Approaches. Journal of Personality, 80(1), 219-251.
- Landsheer, J.A. (2010). The specification of causal models with Tetrad IV: a review. Structural Equation Modeling, 17(4), 703-711.
- Zheng, Z.E., & Pavlou, P.A. (2010). Toward a Causal Interpretation from Observational Data: A New Bayesian Networks Method for Structural Models with Latent Variables. Information Systems Research, 21(2), 365-391.
- Xu, L. (2010). Machine learning problems from optimization perspective. Journal of Global Optimization, 47, 369–401.
- Tu, S., & Xu, L. (2011a). Parameterizations make different model selections: Empirical findings from factor analysis. Frontiers of Electrical and Electronic Engineering in China, 6(2), 256–274.
- Tu, S., & Xu, L. (2011b). An investigation of several typical model selection criteria for detecting the number of signals. Frontiers of Electrical and Electronic Engineering in China, 6(2), 245–255. http://www.cse.cuhk.edu.hk/~lxu/papers/journal/11FEE-tsk-sev.pdf ;
- Xu, L. (2011). Codimensional matrix pairing perspective of BYY harmony learning: hierarchy of bilinear systems, joint decomposition of data-covariance, and applications of network biology. Frontiers of Electrical and Electronic Engineering in China, 6(1), 86–119.
Here are some other references:
- Liu, T., Dai, H., and Zhao, Y. (2012). Comparison of Full-Information and Limited-Information Methods for Bi-Factor Model. Advances in information Sciences and Service Sciences (AISS), 4(11), 11-18.
- Chen, F.F., Sousa, K.H., and West, S.G. (2005). Testing Measurement Invariance of Second-Order Factor Models. Structural Equation Modeling, 12(3), 471-492.
- Resie, S.P, Moore, T.M., and Haviland, M.G. (2010). Bifactor Models and Rotations: Exploring the Extent to which Multidimensional Data Yield Univocal Scale Scores. Journal of Personality Assessement, 92(6), 544–559.
In an older post, I talked about formative vs. reflective measurement. Here are some slides that contain a lot more references.
Book review
Here are some notes on statistical books I read this (academic) year. This time, I will concentrate on psychometrics. Several books rely on Mplus.
-
Introduction to Psychometric Theory (Raykov & Marcoulides, 2011, Routledge). This is an interesting overview of ‘modern’ psychometrics, including factor analysis and item response theory. The authors provide a detailed account of reliability (chapters 6 and 7), and generalizability theory.
-
Data analysis with Mplus (Geiser, 2013, Guilford Press). This is a gentle introduction to the Mplus software for structural equation modeling (cross-sectional and longitudinal settings), latent class analysis and hierarchical multilevel models.
-
Discovering Structural Equation Modeling Using Stata (Acock, 2013, Stata Press). I really like books from Stata Press: they are generally well-written, background information is provided and applications are well targeted and illustrated. I already talked about this book as it was published along the new release of Stata 12 and its SEM builder. As always, additional material are available on the companion website.
-
Structural Equation Modeling. Applications Using Mplus (Wang & Wang, 2012, Wiley). This is a very nice book, with complete Mplus code to illustrate various models fitted on a short version of the Brief Symptoms Inventory (BSI-18).
-
Latent Variable Modeling Using R (Beaujean, 2014, Routledge)