Stata : analyse de la variance
Table des matières
L'analyse de variance (ANOVA), souvent retrouvée dans l'exploitation d'un plan d'expérience, peut être dérivée dans la plupart des cas à partir des modèles de régression vus au chapitre 3 (et plus tard, aux chapitres 9 et 10). Toutefois, une présentation de la décomposition des sources de variance et du calcul des sommes de carré associées, indépendante de l'approche de régression linéaire, est proposée dans ce chapitre, d'autant que Stata dispose de commandes spécifiques pour les modèles d'ANOVA, en particulier oneway et anova.
Dupont [1] consacre plusieurs chapitres de son excellent ouvrage à l'analyse de variance, incluant le cas des mesures répétées.
Analyse de variance à un facteur
Modèle d'ANOVA
Le modèle d'ANOVA à un facteur se formule ainsi :
\[ y_{ij}=\mu_i+\varepsilon_{ij}\qquad i=1,\dots,a;\, j=1,\dots,n, \]
où \(y_{ij}\) désigne la $j$ème observation associée au traitement (ou groupe) \(i\), \(\mu_i\) est la moyenne du traitement et \(\varepsilon_{ij}\) représente la valeur résiduelle. La formulation ci-dessus se nomme "modèle moyen". Si l'on considère les \(\mu_i\) par rapport à la moyenne générale, \(\mu\), avec \(\mu_i = \mu+\tau_i\), alors on peut écrire le modèle sous forme de modèle d'effets :
\[ y_{ij}=\mu + \tau_i+\varepsilon_{ij}\qquad i=1,\dots,a;\, j=1,\dots,n. \]
Les \(\tau_i\) reflètent ainsi les différentes entre les moyennes des traitements et la moyenne générale, et il s'agit bien d'effets au sens propre du terme.
Dans l'exemple suivant, tiré de [1], on s'intéresse à la relation entre l'âge des participants à l'étude au moment du diagnostique et un polymorphisme de séquence. Les données sont disponibles dans le fichier polymorphism.dta :
use data/polymorphism list in 1/5
set more off
use data/polymorphism
list in 1/5
+---------------------+
| id age genotype |
|---------------------|
1. | 1 43 1.6/1.6 |
2. | 2 47 1.6/1.6 |
3. | 3 55 1.6/1.6 |
4. | 4 57 1.6/1.6 |
5. | 5 61 1.6/1.6 |
+---------------------+
Un résumé descriptif des données de groupe (ici défini par le type de polymorphisme) peut être obtenu très rapidement à l'aide de tabstat :
tabstat age, by(genotype) stat(mean sd n)
tabstat age, by(genotype) stat(mean sd n)
Summary for variables: age
by categories of: genotype (Genotype)
genotype | mean sd N
---------+------------------------------
1.6/1.6 | 64.64286 11.18108 14
1.6/0.7 | 64.37931 13.25954 29
0.7/0.7 | 50.375 10.63877 16
---------+------------------------------
Total | 60.64407 13.49427 59
----------------------------------------
Un résumé graphique de la distribution conditionnelle de l'âge dans les trois groupes s'obtient tout aussi simplement à l'aide de graph box :
set scheme plotplain graph box age, over(genotype) graph export "fig-04-boxplot-age-genotype.eps", replace
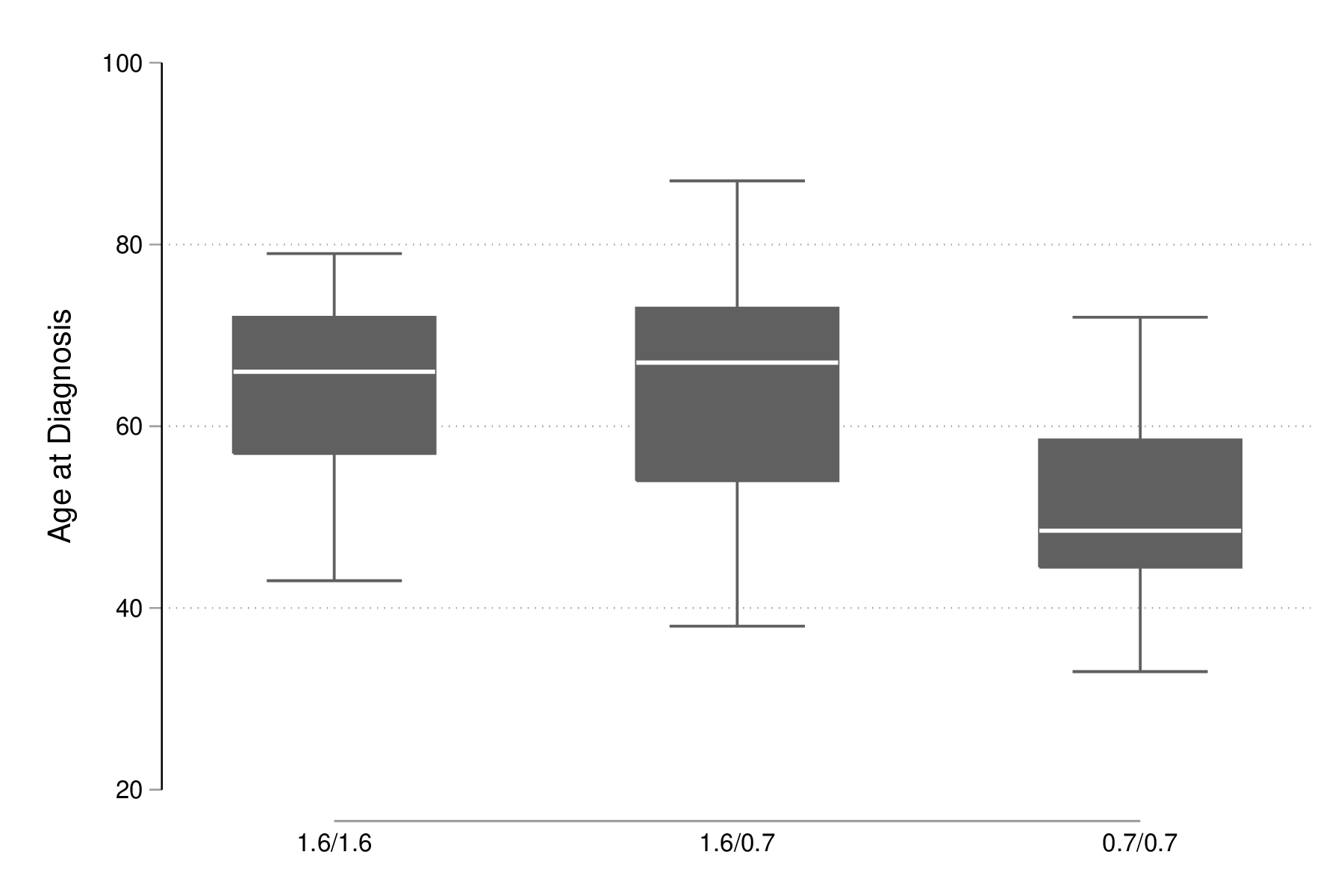
Figure 1 : Histogrammes pour l'âge de diagnostic en fonction du polymorphisme
Il est également possible d'afficher ces distributions sous forme d'histogrammes d'effectifs ou de fréquences, par exemple :
histogram age, by(genotype, col(3)) freq graph export "fig-04-hist-age-genotype.eps", replace
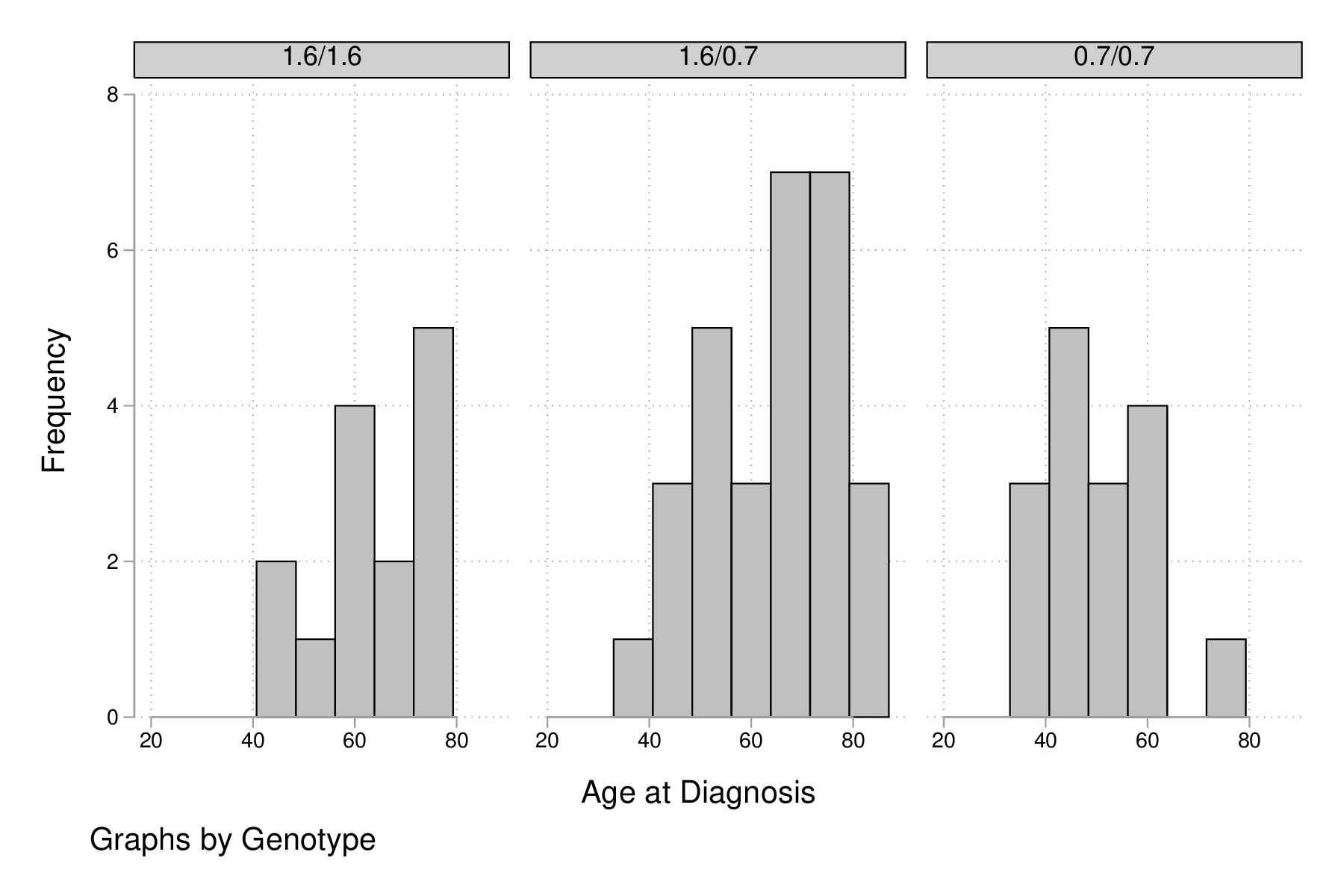
Figure 2 : Distribution de l'âge de diagnostic en fonction du polymorphisme
Le tableau d'ANOVA peut être constuit à l'aide de oneway dans le cas où il n'y a qu'une seule variable explicative. L'option tabulate fournit exactement le même résumé numérique que la commande tabstat ci-dessus, tandis que l'option bonferonni ajoute la comparaison de l'ensemble des paires de moyennes avec une correction de Bonferroni pour les tests multiples. Si l'on ne souhaite que ces derniers, il suffit d'ajouter l'option noanova, mais en règle générale il est préférable de réaliser le test d'ensemble avant d'examiner les tests spécifiques, sauf si l'on a une hypothèse de recherche très particulière.
oneway age genotype
oneway age genotype
Analysis of Variance
Source SS df MS F Prob > F
------------------------------------------------------------------------
Between groups 2315.73355 2 1157.86678 7.86 0.0010
Within groups 8245.79187 56 147.246283
------------------------------------------------------------------------
Total 10561.5254 58 182.095266
Bartlett's test for equal variances: chi2(2) = 1.0798 Prob>chi2 = 0.583
Conditions d'application du test
Il est généralement recommendé de vérifier les hypothèses du modèle, en particulier celle portant sur l'égalité des variances parentes, de manière graphique. Notons que oneway propose d'office un test formel d'égalité des variances (test de Bartlett). Le test de Levenne est disponible via la commande robvar (statistique W50) :
robvar age, by(genotype)
robvar age, by(genotype)
| Summary of Age at Diagnosis
Genotype | Mean Std. Dev. Freq.
------------+------------------------------------
1.6/1.6 | 64.642857 11.181077 14
1.6/0.7 | 64.37931 13.259535 29
0.7/0.7 | 50.375 10.638766 16
------------+------------------------------------
Total | 60.644068 13.494268 59
W0 = 0.83032671 df(2, 56) Pr > F = 0.44120161
W50 = 0.60460508 df(2, 56) Pr > F = 0.54981692
W10 = 0.79381598 df(2, 56) Pr > F = 0.45713722
Concernant la normalité des distributions (parentes), à partir de l'échantillon il est toujours possible de tracer la fonction de répartition des observations, un histogramme ou un diagramme de type boîte à moustaches (cf. section suivante). La commande swilk fournit le test de Shapiro-Wilks, mais comme les méthodes graphiques restent à privilégier, voici une façon de vérifier la normalité des résidus du modèle (dans le cas de l'ANOVA à un facteur, cela ne change pas grand-chose par rapport au fait de travailler sur les observations directement, mais dans le cas à plus d'un facteur en interaction c'est la méthode recommendée) :
quietly anova age genotype predict r, resid qnorm r graph export "fig-04-qnorm-age-genotype-resid.eps", replace
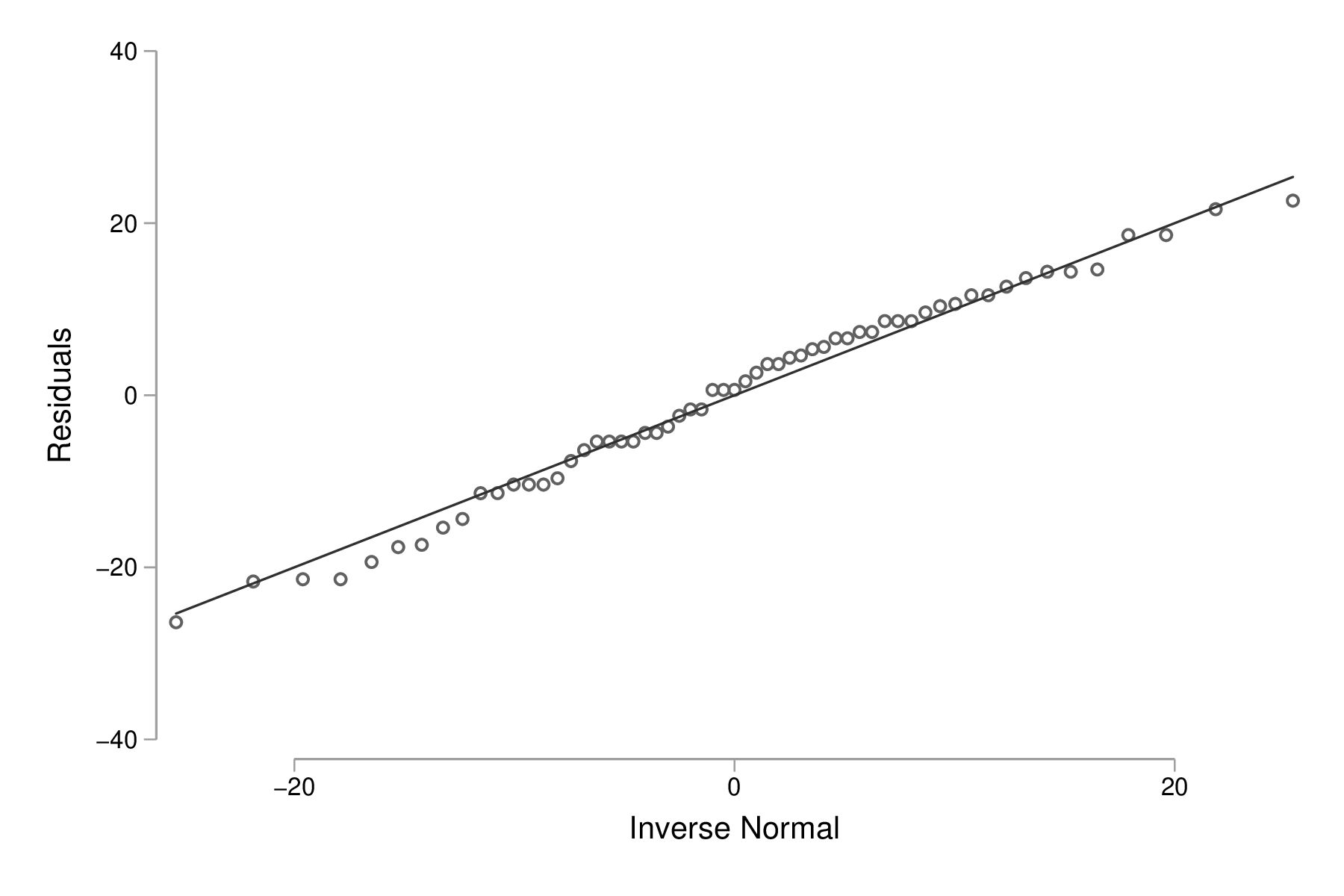
Figure 3 : Distribution des résidus du modèle d'ANOVA
Commandes graphiques
Stata n'offre pas vraiment de commandes graphiques de post-estimation à l'exception de celles applicables au cas du modèle linéaire, telles que les graphiques de résidus en fonction des valeurs prédites ou observées. Il existe toutefois de nombreux packages disponibles sur le site SSC, en particulier la commande anovaplot (une approche manuelle pour construire un graphique d'interaction est présentée dans la section suivante) :
anovaplot graph export "fig-04-anovaplot-age-genotype.eps", replace
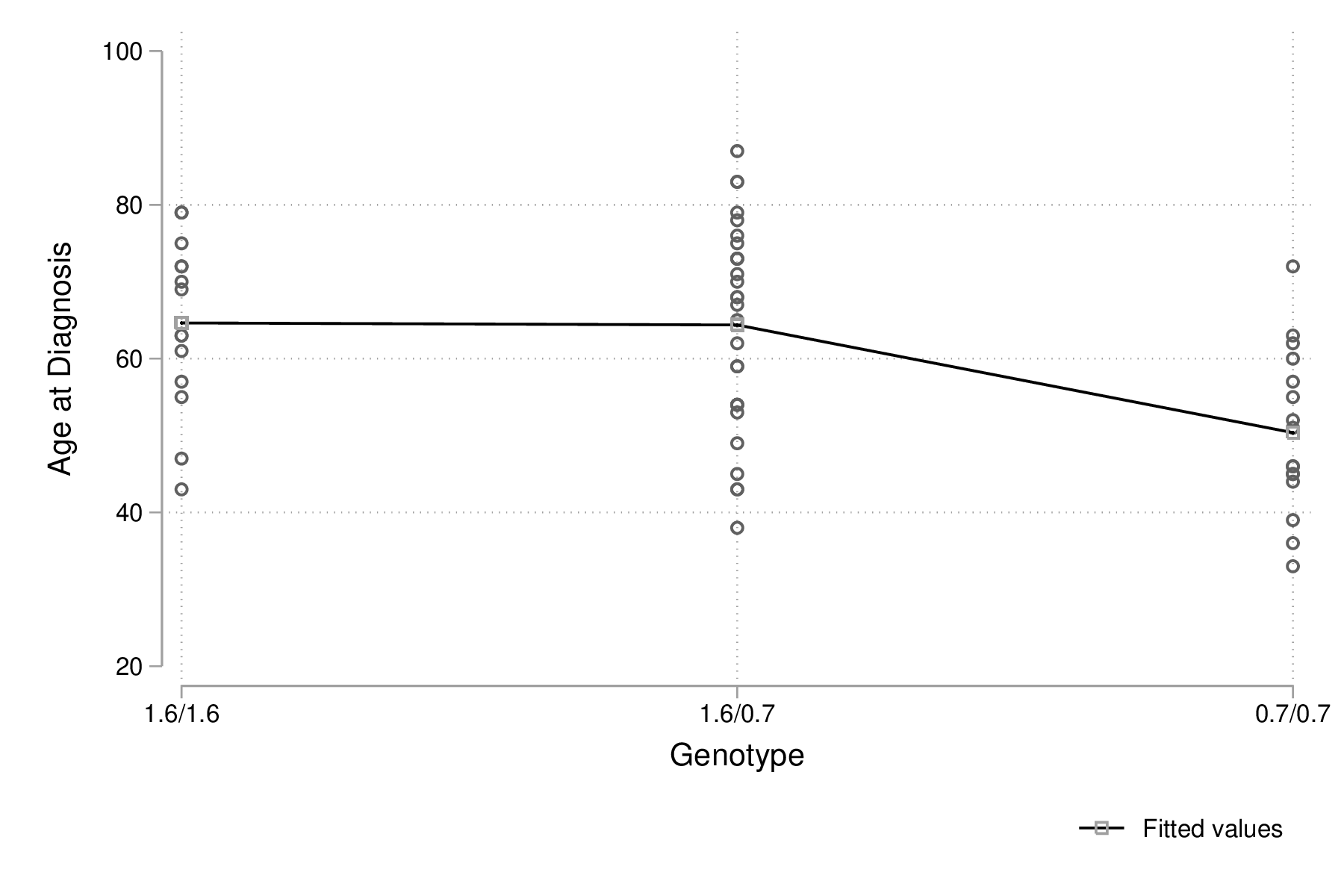
Figure 4 : Valeurs prédites par le modèle d'ANOVA
Une référence intéressante concernant les approches graphiques pour le diagnostique des modèles de régression, au sens large, est l'article de [2].
Comparaisons multiples
Lorsque le résultat du test d'ANOVA est significatif, il est souvent intéressant, voire nécessaire d'aller inspecter le résultat des comparaisons de chaque paire de moyennes. Comme indiqué plus haut, il est déconseillé de procéder à de telles comparaisons multiples lorsque l'ANOVA n'est en elle-même pas significative puisque dans ce cas il s'agit un peu de ce que l'on appelle du "data fishing". Cela dit, dans certains cas de figure, il est possible de pré-spécifier les comparaisons d'intérêt et de n'analyser que ces contrastes d'intérêt. Dans ce cas, le modèle d'ANOVA est même facultatif.
Il y a deux manières de procéder pour réaliser des comparaisons de paires de moyennes sous Stata (outre la comparaison manuelle à l'aide de ttest): (1) la commande oneway offre une option permettant de tester les paires de moyennes et d'appliquer une correction pour borner le risque d'erreur d'ensemble (FWER) ; (2) les commandes pwcompare, contrast ou lincome (ou test). La commande margins fournit plus de souplesse dans l’estimation conditionnelle ou marginale des effets et permet en outre la représentation graphique des résultats grâce à marginsplot. En dehors de pwcompare, les autres commandes restent applicables dans le cas du modèle linéaire dans son ensemble.
Voici le résultat des tests multiples à partir de oneway :
oneway age genotype, bonferroni noanova
oneway age genotype, bonferroni noanova
Comparison of Age at Diagnosis by Genotype
(Bonferroni)
Row Mean-|
Col Mean | 1.6/1.6 1.6/0.7
---------+----------------------
1.6/0.7 | -.263547
| 1.000
|
0.7/0.7 | -14.2679 -14.0043
| 0.007 0.001
On arriverait naturellement aux mêmes conclusions en construisant manuellement les tests de Student correspondants, moyennant la prise en compte de la bonne somme de carrés (variance "poolée") :
quietly ttest age if genotype != 1, by(genotype) display r(p)*3
quietly ttest age if genotype != 1, by(genotype) 00228566
L'ANOVA via la régression
The regress command is used to fit the underlying regression model corresponding to an ANOVA model fit using the anova command. Type regress after anova to see the coefficients, standard errors, etc., of the regression model for the last run of anova.
quietly anova age genotype regress
quietly anova age genotype
regress
Source | SS df MS Number of obs = 59
-------------+------------------------------ F( 2, 56) = 7.86
Model | 2315.73355 2 1157.86678 Prob > F = 0.0010
Residual | 8245.79187 56 147.246283 R-squared = 0.2193
-------------+------------------------------ Adj R-squared = 0.1914
Total | 10561.5254 58 182.095266 Root MSE = 12.135
------------------------------------------------------------------------------
age | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
genotype |
1.6/0.7 | -.2635468 3.949057 -0.07 0.947 -8.174458 7.647365
0.7/0.7 | -14.26786 4.440775 -3.21 0.002 -23.1638 -5.371915
|
_cons | 64.64286 3.243084 19.93 0.000 58.14618 71.13953
------------------------------------------------------------------------------
Cas des variances non égales
Plusieurs généralisations du test de Welch dans le cas où les variances ne sont pas égales ont été proposées [3]. Sous Stata, les procédures wtest et fstar peuvent être téléchargées. Voici un exemple d'application avec wtest, dont les auteurs ont montré que cette statistique de test convient dans le cas où les échantillons sont de même taille (ce n'est pas vraiment le cas ici) mais de variance différente [4] :
wtest age genotype
wtest age genotype unrecognized command: wtest r(199);
Approche non paramétrique
L'ANOVA de Kruskal-Wallis, qui généralise la commande ranksum au cas à plus de deux échantillons, est disponible via la commande kwallis :
kwallis age, by(genotype)
kwallis age, by(genotype) Kruskal-Wallis equality-of-populations rank test +---------------------------+ | genotype | Obs | Rank Sum | |----------+-----+----------| | 1.6/1.6 | 14 | 494.00 | | 1.6/0.7 | 29 | 999.50 | | 0.7/0.7 | 16 | 276.50 | +---------------------------+ chi-squared = 12.060 with 2 d.f. probability = 0.0024 chi-squared with ties = 12.073 with 2 d.f. probability = 0.0024
Cette commande ne dispose pas d'option. On peut retrouvera simplement les sommes des rangs (voire les moyennes) utilisées dans ce test statistique à l'aide des instructions suivantes :
egen rr = rank(age) bysort genotype : egen rs = sum(rr) tabdisp genotype, cellvar(rs) format(%3.1f)
egen rr = rank(age) bysort genotype : egen rs = sum(rr) tabdisp genotype, cellvar(rs) format(%3.1f) ---------------------- Genotype | rs ----------+----------- 1.6/1.6 | 494.0 1.6/0.7 | 999.5 0.7/0.7 | 276.5 ----------------------
Il est également possible de coupler cette instruction avec une série de tests post-hoc de Mann-Whitney, comme illustré ci-dessous :
foreach k of numlist 1/3 {
quietly ranksum age if genotype != `k', by(genotype)
display r(z), "(p=" 2*(1-normal(r(z))) ")"
}
05188301 (p=.95862192)
Analyse de variance à plusieurs facteurs
Utilisation de la commande anova
La commande oneway est limité au cas à un facteur explicatif. La commande anova est plus générale et couvre : les plans factoriels et emboîtés, les plans équilibrés ou non (cf. calcul des sommes de carrés), les mesures répétées, l’analyse de covariance. Dans le cas à un facteur à effet fixe, on retrouvera évidemment les mêmes résultats que plus haut :
anova age genotype
anova age genotype
Number of obs = 59 R-squared = 0.2193
Root MSE = 12.1345 Adj R-squared = 0.1914
Source | Partial SS df MS F Prob > F
-----------+----------------------------------------------------
Model | 2315.73355 2 1157.86678 7.86 0.0010
|
genotype | 2315.73355 2 1157.86678 7.86 0.0010
|
Residual | 8245.79187 56 147.246283
-----------+----------------------------------------------------
Total | 10561.5254 58 182.095266
Les comparaisons par paires de moyennes s’obtiennent à l’aide de pwcompare, commande plus générale que pwmean. Les options de correction (mcompare()) incluent en plus : tukey, snk, duncan et dunnett.
pwcompare genotype, cformat(%3.2f)
pwcompare genotype, cformat(%3.2f)
Pairwise comparisons of marginal linear predictions
Margins : asbalanced
---------------------------------------------------------------------
| Unadjusted
| Contrast Std. Err. [95% Conf. Interval]
--------------------+------------------------------------------------
genotype |
1.6/0.7 vs 1.6/1.6 | -0.26 3.95 -8.17 7.65
0.7/0.7 vs 1.6/1.6 | -14.27 4.44 -23.16 -5.37
0.7/0.7 vs 1.6/0.7 | -14.00 3.78 -21.57 -6.43
---------------------------------------------------------------------
Voici un exemple de plan d'expérience dans lequel on s'intéresse à la fabrication d'une batterie capable de fonctionner dans des conditions extrêmes de température [5]. Cette étude comprend deux facteurs expérimentaux ayant trois niveaux chacun : la température (°F) et un paramètre lié au design de la batterie elle-même. Il s'agit donc d'un plan factoriel \(3^2\). Les données sont disponibles dans le fichier battery.txt.
import delimited "data/battery.txt", delimiter("", collapse) varnames(1) clear
list in 1/3
r
(3 vars, 36 obs)
list in 1/3
+----------------------------+
| life material temper~e |
|----------------------------|
1. | 130 1 15 |
2. | 74 1 15 |
3. | 155 1 15 |
+----------------------------+
Voici les résultats pour le modèle avec interaction :
anova life material##temperature
anova life material##temperature
Number of obs = 36 R-squared = 0.7652
Root MSE = 25.9849 Adj R-squared = 0.6956
Source | Partial SS df MS F Prob > F
---------------------+----------------------------------------------------
Model | 59416.2222 8 7427.02778 11.00 0.0000
|
material | 10683.7222 2 5341.86111 7.91 0.0020
temperature | 39118.7222 2 19559.3611 28.97 0.0000
material#temperature | 9613.77778 4 2403.44444 3.56 0.0186
|
Residual | 18230.75 27 675.212963
---------------------+----------------------------------------------------
Total | 77646.9722 35 2218.48492
On rappelle que le modèle à effets pour ce type d'ANOVA s'écrit :
\[ y_{ijk}=\mu+\tau_i+\beta_j+(\tau\beta)_{ij}+\varepsilon_{ijk}, \]
où \(i\), \(j\) (\(i=1\dots a\), \(j=1\dots b\)) décrivent les niveaux des facteurs \(A\) et \(B\), et \(k\) représente le numéro d'observation (\(k=1\dots n\)). L'ordre dans lequel les observations sont choisies est tiré au sort, de sorte que l'on parle d'un plan complètement randomisé. On distingue \(a+b+1\) dépendances linéaires dans ce système d'équations, et par conséquent les paramètres ne peuvent être identifiés sans imposer certaines contraintes. En règle générale, on impose \(\sum_{i=1}^a\hat{\tau}_i=0\), \(\sum_{j=1}^b\hat{\beta}_j=0\), \(\sum_{i=1}^a\widehat{\tau\beta}_{ij}=0\) (\(j=1,2,\dots,b\)) et \(\sum_{j=1}^b\widehat{\tau\beta}_{ij}=0\) (\(i=1,2,\dots,a\)). On montre avec un peu d'algèbre que l'équation ci-dessus peut être exprimée sous la forme d'une somme corrigée de sommes de carrés :
\[ \begin{split} \sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^n(y_{ijk}-\bar{y}_{\cdot\cdot\cdot})^2 &= \sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^n[ (\bar{y}_{i\cdot\cdot}-\bar{y}_{\cdot\cdot\cdot})+(\bar{y}_{\cdot j\cdot}-\bar{y}_{\cdot\cdot\cdot}) \\ & \quad + (\bar{y}_{ij\cdot}-\bar{y}_{i\cdot\cdot}-\bar{y}_{\cdot j\cdot}+\bar{y}_{\cdot\cdot\cdot})+(y_{ijk}-\bar{y}_{ij\cdot})]^2\\ &= bn\sum_{i=1}^a(\bar{y}_{i\cdot\cdot}-\bar{y}_{\cdot\cdot\cdot})^2+an\sum_{j=1}^b(\bar{y}_{\cdot j\cdot}-\bar{y}_{\cdot\cdot\cdot})^2 \\ & \quad + n\sum_{i=1}^a\sum_{j=1}^b(\bar{y}_{ij\cdot}-\bar{y}_{i\cdot\cdot}-\bar{y}_{\cdot j\cdot}+\bar{y}_{\cdot\cdot\cdot})^2\\ & \quad + \sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^n(y_{ijk}-\bar{y}_{ij\cdot})^2 \end{split} \]
Sous forme symbolique, et on retrouve la formule passée en arguments de anova (sans la résiduelle), on a bien \(SS_T=SS_A+SS_B+SS_{AB}+SS_E\). Les hypothèses associées à ce type de plan portent généralement sur les effets principaux et sur l'effet d'interaction :
- égalité des effets du traitement en lignes, \(H_0:\; \tau_1=\tau_2=\dots=\tau_a=0\) ;
- égalité des effets du traitement en colonnes, \(H_0:\; \beta_1=\beta_2=\dots=\beta_b=0\) ;
- absence d'interaction entre les traitements en lignes et en colonnes, \(H_0:\; (\tau\beta)_{ij}=0\quad \textrm{for all}\; i,j\).
Voici le tableau résumant les moyennes pour chaque traitement, ainsi que les écart-types et effectifs associés. On pourra vérifier que le plan est parfaitement équilibré :
table material temperature, contents(mean life sd life n life) format(%4.1f)
table material temperature, contents(mean life sd life n life) format(%4.1f)
-------------------------------
| Temperature
Material | 15 70 125
----------+--------------------
1 | 134.8 57.2 57.5
| 45.4 23.6 26.9
| 4 4 4
|
2 | 155.8 119.8 49.5
| 25.6 12.7 19.3
| 4 4 4
|
3 | 144.0 145.8 85.5
| 26.0 22.5 19.3
| 4 4 4
-------------------------------
Un graphique d'interaction permettant d'illustrer les variations de moyennes entre les conditions pourrait être constuit à l'aide de scatter comme suit :
preserve collapse (mean) mean=life (sd) sd=life, by(material temperature) list in 1/3 drop sd reshape wide mean, i(temperature) j(material) twoway connected mean* temperature, legend(label(1 "#1") label(2 "#2") label(3 "#3")) ytitle(Mean life) restore
Il existe également les commandes rcap et serrbar pour gérer les barres d'erreur. Toutefois la commande marginplot est beaucoup plus souple d'utilisation et elle s'interface directement avec les modèles statistiques les plus courants. Voici une exemple de son utilisation avec le modèle précédent :
quietly margins temperature#material marginsplot, name(p) graph export "fig-04-margins-life-battery.eps", replace name(p)
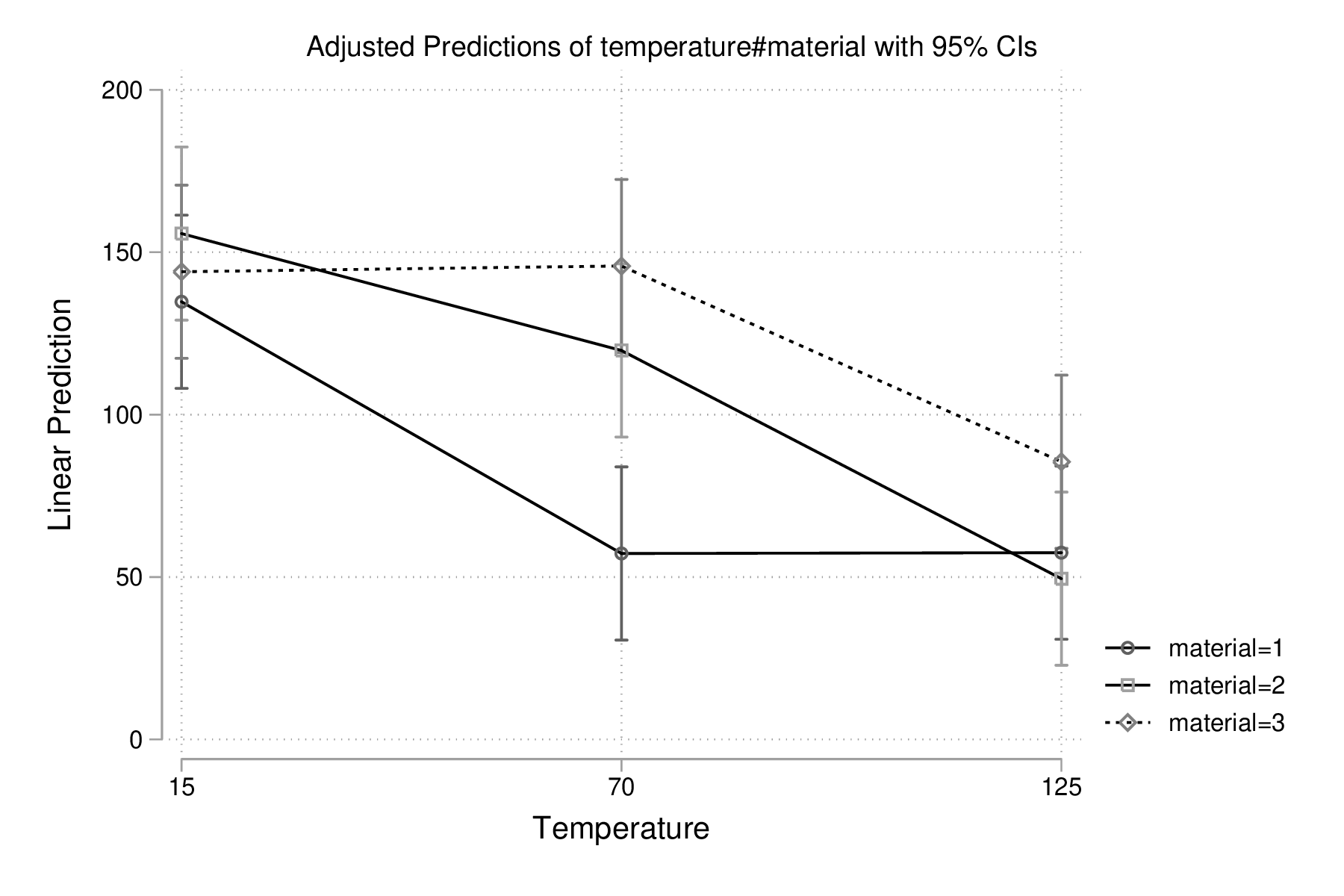
Figure 5 : Graphique d'interaction avec la commande marginsplot
Définition et analyse de contrastes
Voyons ce que l'on peut réaliser en termes de tests de contrastes à l'aide de pwcompare. Dans un premier temps, la comparaison de l'ensemble des paires de moyennes peut être réalisée en décomposant le terme d'interaction, et en utilisant la méthode de Tukey comme correction pour les tests multiples :
pwcompare material#temperature, mcompare(tukey)
pwcompare material#temperature, mcompare(tukey)
Pairwise comparisons of marginal linear predictions
Margins : asbalanced
-----------------------------------
| Number of
| Comparisons
---------------------+-------------
material#temperature | 36
-----------------------------------
----------------------------------------------------------------------
| Tukey
| Contrast Std. Err. [95% Conf. Interval]
---------------------+------------------------------------------------
material#temperature |
(1 70) vs (1 15) | -77.5 18.37407 -139.3232 -15.67681
(1 125) vs (1 15) | -77.25 18.37407 -139.0732 -15.42681
(2 15) vs (1 15) | 21 18.37407 -40.82319 82.82319
(2 70) vs (1 15) | -15 18.37407 -76.82319 46.82319
(2 125) vs (1 15) | -85.25 18.37407 -147.0732 -23.42681
(3 15) vs (1 15) | 9.25 18.37407 -52.57319 71.07319
(3 70) vs (1 15) | 11 18.37407 -50.82319 72.82319
(3 125) vs (1 15) | -49.25 18.37407 -111.0732 12.57319
(1 125) vs (1 70) | .25 18.37407 -61.57319 62.07319
(2 15) vs (1 70) | 98.5 18.37407 36.67681 160.3232
(2 70) vs (1 70) | 62.5 18.37407 .6768132 124.3232
(2 125) vs (1 70) | -7.75 18.37407 -69.57319 54.07319
(3 15) vs (1 70) | 86.75 18.37407 24.92681 148.5732
(3 70) vs (1 70) | 88.5 18.37407 26.67681 150.3232
(3 125) vs (1 70) | 28.25 18.37407 -33.57319 90.07319
(2 15) vs (1 125) | 98.25 18.37407 36.42681 160.0732
(2 70) vs (1 125) | 62.25 18.37407 .4268132 124.0732
(2 125) vs (1 125) | -8 18.37407 -69.82319 53.82319
(3 15) vs (1 125) | 86.5 18.37407 24.67681 148.3232
(3 70) vs (1 125) | 88.25 18.37407 26.42681 150.0732
(3 125) vs (1 125) | 28 18.37407 -33.82319 89.82319
(2 70) vs (2 15) | -36 18.37407 -97.82319 25.82319
(2 125) vs (2 15) | -106.25 18.37407 -168.0732 -44.42681
(3 15) vs (2 15) | -11.75 18.37407 -73.57319 50.07319
(3 70) vs (2 15) | -10 18.37407 -71.82319 51.82319
(3 125) vs (2 15) | -70.25 18.37407 -132.0732 -8.426813
(2 125) vs (2 70) | -70.25 18.37407 -132.0732 -8.426813
(3 15) vs (2 70) | 24.25 18.37407 -37.57319 86.07319
(3 70) vs (2 70) | 26 18.37407 -35.82319 87.82319
(3 125) vs (2 70) | -34.25 18.37407 -96.07319 27.57319
(3 15) vs (2 125) | 94.5 18.37407 32.67681 156.3232
(3 70) vs (2 125) | 96.25 18.37407 34.42681 158.0732
(3 125) vs (2 125) | 36 18.37407 -25.82319 97.82319
(3 70) vs (3 15) | 1.75 18.37407 -60.07319 63.57319
(3 125) vs (3 15) | -58.5 18.37407 -120.3232 3.323187
(3 125) vs (3 70) | -60.25 18.37407 -122.0732 1.573187
----------------------------------------------------------------------
Le test d'un contraste spécifique peut être réalisé tout aussi simplement, en indiquant le niveau du ou des facteurs qui nous intéressent, ainsi que les degrés de liberté associés :
pwcompare i2.material#i3.temperature, mcompare(tukey) df(34)
pwcompare i2.material#i3.temperature, mcompare(tukey) df(34) level 3 of factor temperature not found in list of covariates r(111);
Des simulations de Monte Carlo permettent évaluer la puissance statistique d'un plan factoriel, en spécifiant les valeurs attendues pour les moyennes et variances dans chacune des conditions expérimentales. Il ne s'agit donc pas d'un calcul de puissance a posteriori.
Autres plans d'expérience
Plan en blocs complets randomisés
Les plans en blocs complets randomisés (RCBD en anglais) sont utilisés lorsque l'on souhaite contrôler certains facteurs de nuisance. Le facteur d'intérêt est alors appelé traitement et le ou les facteurs de nuisance bloc(s). Il ne faut pas les confondre avec les modèles d'analyse de covariance dans lesquels les réponses sont ajustées a posteriori pour prendre en compte les facteurs de nuisance.
Block what you can; randomize what you cannot. — George E.P. Box
Les conditions de validité associées à ce type d'analyse sont les mêmes que dans le cas de l'ANOVA à plusieurs facteurs (indépendance, normalité et homogénéité des variances), mais on postule également l'absence d'interaction entre traitement et bloc (additivité des effets) et la symétrie composée de la matrice de variance-covariance, comme dans le cas de l'ANOVA à mesures répétées (dans cette dernière, les sujets sont assimilables aux blocs, mais chaque bloc contient plusieurs sujets appariés sur une ou plusieurs caractéristiques communes).
Le modèle à effet se formule ainsi :
\[ y_{ij}=\mu+\tau_i+\beta_j+\varepsilon_{ij}\qquad (i=1,2,\dots,a; j=1,2,\dots,b), \]
avec les contraintes \(\sum_{i=1}^a\tau_i = 0\) et \(\sum_{j=1}^b\beta_j = 0\). L'équation fondamentale de cette ANOVA revient donc à \(SS_T=SS_{\textrm{treat}}+SS_{\textrm{block}}+SS_E\). La résiduelle à \((a-1)(b-1)\) degrés de liberté capture la variance non expliquée par les facteurs considérés.
Considérons l'exemple suivant, tiré de
Plan en blocs incomplets équilibrés
Les plans en blocs incomplets équilibrés (BIBD en anglais) font partie des plans en blocs aléatoires dans lesquels certains traitements ne sont pas observés pour certains blocs ou combinaisons de blocs. Si l'on note \(a\) le nombre de traitements, et \(k\) le nombre maximum de traitements dans chaque bloc (\(k < a\)), alors un plan BIBD se résume à un arrangement de \(a \choose k\) combinaisons [6].
Voici un exemple discuté par Montgomery, chapitre 4 [5] :
| Traitement | 1 | 2 | 3 | 4 | \(y_{i\cdot}\) |
|---|---|---|---|---|---|
| 1 | 73 | 74 | -- | 71 | 218 |
| 2 | -- | 75 | 67 | 72 | 214 |
| 3 | 73 | 75 | 68 | -- | 216 |
| 4 | 75 | -- | 72 | 75 | 222 |
| \(y_{\cdot j}\) | 221 | 224 | 207 | 218 | \(870=y_{\cdot\cdot}\) |
Si l'on considère qu'il y a \(a\) traitements et \(b\) blocs, et que chaque bloc consiste en \(k\) traitements, avec \(r\) répliques au total dans le plan, alors on a \(N = ar = bk\) observations, et le nombre de fois où chaque paire de traitement apparaît dans le même bloc vaut \(\lambda = \frac{r(k-1)}{a-1}\), \(\lambda\in \{0,1,2,\dots\}\). Si \(a = b\), le plan est dit symétrique. 1
use data/tab-4-21, clear
use data/tab-4-21, clear
.dta too modern
File data/tab-4-21.dta is from a more recent version of Stata. Type
update query to determine whether a free update of Stata is available,
and browse http://www.stata.com/ to determine if a new version is
available.
r(610);
Références
| [1] | W. D. Dupont, Statistical Modeling for Biomedical Researchers. Cambridge University Press, 2nd ed., 2009. |
| [2] | N. Cox, “Speaking stata: Graphing model diagnostics,” The Stata Journal, vol. 4, no. 4, pp. 449--475, 2004. |
| [3] | B. L. Welch, “On the comparison of several mean values: an alternative approach,” Biometrika, vol. 38, p. 330—336, 1951. |
| [4] | R. Wilcox, V. Charlin, and K. Thompson, “New monte carlo results on the robustness of the ANOVA f, W and F statistics,” vol. 15, no. 4, pp. 933--943, 1986. |
| [5] | D. C. Montgomery, Design and Analysis of Experiments. Wiley, 5 ed., 2001. |
| [6] | K. Hinkelmann and O. Kempthorne, Design and Analysis of Experiments. Volume 2: Advanced Experimental Design. John Wiley & Sons, Inc., 2005. |
Notes de bas de page:
Comme \(\lambda\) est forcément un entier, cela limite l'espace des solutions pour certains plans. Par exemple, les contraintes \(r=4\), \(t=4\), \(b=8\) et \(k=2\) ne sont pas admissibles dans un simple plan en blocs aléatoires, mais restent valides dans le cas un plan en blocs incomplets équilibrés.