
R dispose des fonctionnalités usuelles concernant les structures de contrôle (boucle ou itération, branchement conditionnel).
for (i in 1:5) print(i)## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5L'indentation n'est pas obligatoire mais facilite évidemment la lisibilité. Lorsqu'il y a plus d'une commande, il est nécessaire de les encadrer par des accolades, comme ceci
for (i in 1:5) {
j <- i + 1
print(j)
}## [1] 2
## [1] 3
## [1] 4
## [1] 5
## [1] 6On peut imaginer des situations "plus intéressantes", comme par exemple sélectionner les valeurs prises par une variable selon les modalités d'une autre variable. Par exemple,
f <- factor(sample(rep(c("low", "high"), each = 5)))
x <- sample(1:100, size = length(f))
for (grp in c("low", "high")) print(mean(x[f == grp]))## [1] 27.4
## [1] 67.4Il est nécessaire d'utiliser la commande print pour afficher les résultats générés à l'intérieur de la boucle for. On peut en revanche vouloir stocker les résultats dans une nouvelle variable.
res <- NULL
for (i in levels(f)) res <- append(res, mean(x[f == i]))
names(res) <- levels(f)
res## high low
## 67.4 27.4Les commandes ci-dessus se simplifient, comme beaucoup d'autres instructions faisant appel à des boucles, à l'aide de la commande tapply :
tapply(x, f, mean)## high low
## 67.4 27.4Supposons que l'on dispose de 10 mesures continues, comprises dans l'intervalle [0;10], et que l'on souhaite les filtrer selon leur valeur. Par exemple, toutes les valeurs inférieures ou égales à 5 seront recodées en 0, et toutes les valeurs supérieures à 5 en 1. Voici une première solution possible :
x <- runif(10, min = 0, max = 10)
x## [1] 1.64077 6.24841 9.92185 7.77434 2.66555 2.42659 9.44768 9.45820 0.05168
## [10] 7.06471x[x <= 5] <- 0
x[x != 0] <- 1
x## [1] 0 1 1 1 0 0 1 1 0 1Une solution plus élégante consiste à utiliser la commande ifelse, comme ceci :
ifelse(x <= 5, 0, 1)Il est souvent utile de pouvoir simuler des données. R dispose de générateurs de nombres aléatoires pour la plupart des lois de probabilités utiles en statistique. Avant toute chose, et pour s'assurer de la reproducibilité des résultats, il est nécessaire d'initialiser le générateur (plus exactement, fixer la graine du générateur congruentiel) à l'aide la commande set.seed. Ceci nous assure que lorsque nous lancerons une nouvelle sessions R, les mêmes nombres aléatoires seront générés.
Prenons l'exemple de la loi normale : la commande rnorm permet de générer un nombre quelconque d'aléas gaussiens. Par défaut, la loi normale centrée-réduite (de moyenne 0 et d'écart-type 1) est utilisée.
set.seed(101)
n <- 30
x <- rnorm(n, mean = 12, sd = 2)
head(x)## [1] 11.35 13.10 10.65 12.43 12.62 14.35Il existe également des générateurs de nombres aléatoires tirés dans une loi binomiale (utile pour jouer à pile ou face) ou uniforme. Par exemple,
x <- runif(n)
y <- 0.8 + 1.2 * x + rnorm(n)
dfrm <- data.frame(x, y)
rm(x, y)
xyplot(y ~ x, data = dfrm)
On peut en profiter pour vérifier à quoi ressemble la distribution d'échantillonnage d'une moyenne.
x <- colMeans(replicate(1000, rnorm(n, 10)))
histogram(~x)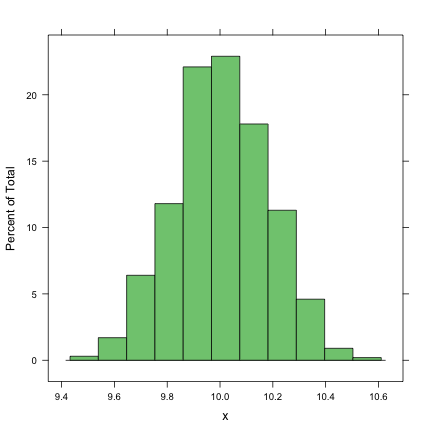
summary(x)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 9.48 9.88 10.00 10.00 10.10 10.60sd(x)## [1] 0.1773Il ne faut pas se laisser impressionner par la succession de commandes imbriquées les unes dans les autres, et procéder par une lecture des commandes les plus imbriquées. Dans l'exemple précédent, colMeans(replicate(1000, rnorm(n, 10))), on a en fait les instructions suivantes :
rnorm(n, 10) : génère n=30 aléas gaussiens de moyenne 10 et d'écart-type 1 (qui est la valeur par défaut) ;replicate(1000, ...) : répète l'instruction en (1) 1000 fois et stocke les résultats dans un tableau de dimensions n x 1000 (lignes x colonnes) ;colMeans(...) : calcule la moyenne de chaque colonne.On a donc au final générer 1000 variables avec 30 observations chacune et calculer les moyennes correspondantes. La moyenne de ces moyennes vaut approximativement la moyenne théorique, et l'écart-type des moyennes observées vaut approximativement \(s/\sqrt{n}\), où \(s\) est l'estimé de l'écart-type de population, \(\sigma\) (en pratique, il est nécessaire de considérer que l'on travaille avec des populations de taille infinie).
Comme on l'a vu, R dispose de commandes pour générer des nombres aléatoires à partir de différentes lois de probabilités. Ces commandes sont préfixées avec un r, suivi du nom abrégé de la loi : runif (uniforme), rnorm (normale), rbinom (binomiale), rpois (Poisson), etc. De même, on peut afficher la densité de probabilité des lois connues de R en utilisant le préfixe d (pour distribution). Par exemple,
q <- seq(-6, 6, by = 0.1)
dn <- dnorm(q)
xyplot(dn ~ q, type = c("l", "g"), xlab = "", ylab = "")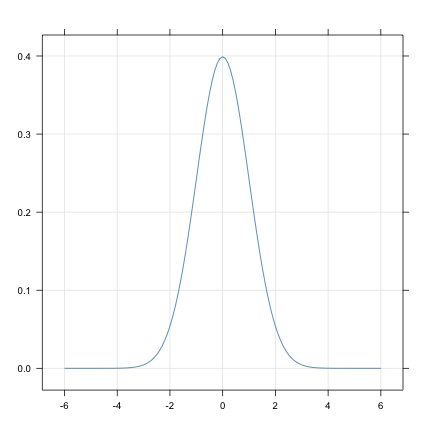
Les options type=c("l","g") indique que l'on souhaite représenter les données sous forme d'une ligne continue, tout en affichant une grille.
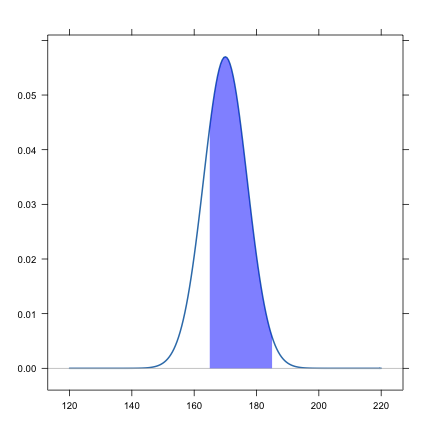
Il est également possible de calculer les quantiles ou fractiles associés à une certaine probabilité (\(x\) tel que \(P(X\leq x)=p\), \(p\) donné), ou réciproquement les valeurs de probabilités (\(p\) telle que \(P(X\leq x)\), \(x\) donné). Pour cela, on utilisera les préfixes q et p, respectivement. Considérons l'exemple suivant : on sait que dans la population française, les garçons âgés de 20 à 35 ans mesurent en moyenne 170 cm, et que la distribution des tailles est normale avec un écart-type de 7 cm.
qnorm(0.975, mean = 170, sd = 7)## [1] 183.7pnorm(185, 170, 7) - pnorm(165, 170, 7)## [1] 0.7464pnorm(150, 170, 7)## [1] 0.002137pnorm(150, 170, 7, lower.tail = FALSE) # 1 - pnorm(150, 170, 7)## [1] 0.9979La deuxième série de commandes retourne en fait la probabilité d'observer une taille comprise entre 165 et 185 cm pour un individu tiré aléatoirement dans la population (des garçons âgés de 20 à 35 ans).
Le niveau de mémoire en fonction de l'âge.
Il s'agit d'une étude décrite dans Eysenck (1974) qui visait à comparer les niveaux de mémoire de sujets plus jeunes ou plus âgés. Eysenck souhaitait tester l'hypothèse selon laquelle quand les sujets devaient traiter des informations verbales (listes de mots), les sujets plus âgés procédaient à un traitement plus réduit et se rappelaient dès lors moins de mots (cette étude a également montré que les deux groupes d'âge ne se distinguaient pas sur le plan de la mémoire lorsqu'aucun traitement en profondeur n'était nécessaire).
Les données contenues dans le fichier eysenck74.dat ont été conçues de manière à présenter les mêmes moyennes et écart-types que deux des conditions de l'étude de Eysenck ; elles font référence à des groupes invités à mémoriser des mots de manière à se les rappeler par la suite. La variable dépendante est le nombre d'éléments rappelés correctement.
Le chargement des données ne pose pas de problème particulier et on utilise la commande read.table qui permet de lire des données stockées dans des fichiers texte. Par défaut, elle suppose que le séparateur de champ est une tabulation et qu'il n'y a pas de ligne d'en-tête, mais il est possible de paramétrer la commande différemment si besoin. Si on ouvre le fichier texte sous un éditeur, on peut vérifier qu'a priori toutes les valeurs sont stockées sous forme numérique :
01 1 21
02 1 19
03 1 17
04 1 15
05 1 22On demandera donc explicitement à R de traiter les deux premières colonnes (variables) comme des variables qualitatives (factor) et la dernière comme une variable quantitative (numeric). On en profitera également pour donner des noms aux variables et recoder les niveaux ou modalités de la variable Age.
eysenck <- read.table("../data/eysenck74.dat", colClasses = c("factor", "factor",
"numeric"))
names(eysenck) <- c("ID", "Age", "Mots")
levels(eysenck$Age) <- c("-", "+")
summary(eysenck)## ID Age Mots
## 01 : 1 -:10 Min. : 5.0
## 02 : 1 +:10 1st Qu.:11.0
## 03 : 1 Median :15.5
## 04 : 1 Mean :15.7
## 05 : 1 3rd Qu.:19.5
## 06 : 1 Max. :22.0
## (Other):14Outre le résumé numérique global, on peut s'intéresser à la distribution de la variable réponse (nombre de mots rappelés dans la tâche de mémorisation) dans les deux groupes de sujets. À l'image d'un histogramme, la commande densityplot permet de visualiser la distribution des observations. La notation ~ Mots | Age signifie en fait que l'on souhaite mettre en relation les distributions univariées de la variable Mots avec les modalités de la variable Age.
densityplot(~Mots | Age, data = eysenck)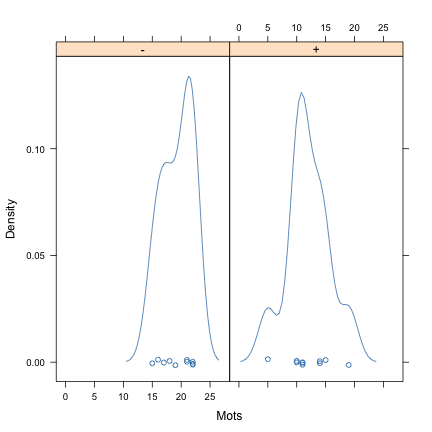
Il est également possible d'afficher sous forme graphique l'équivalent du résumé numérique en 5 points que renverrait la commande summary si elle était appliquée à chacun des groupes (par exemple, tapply(Mots, Age, summary)) : la commande bwplot génère en effet des diagrammes de type boîte à moustaches.
bwplot(Mots ~ Age, data = eysenck)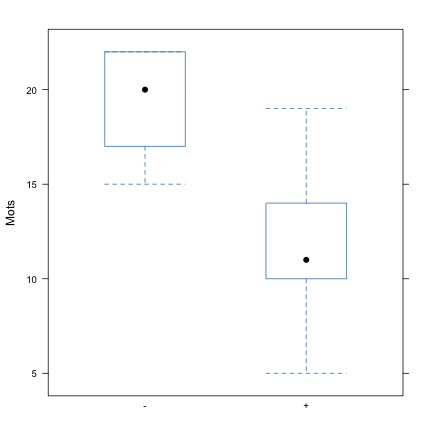
L'inspection des graphiques précédents ne suggère pas d'anormalités particulières dans les distributions empiriques, et l'examen des indicateurs de dispersion suggère que les variances sont à peu près comparables :
with(eysenck, tapply(Mots, Age, sd))## - +
## 2.669 3.742On mettra en oeuvre un test t pour échantillons indépendants, comme suit.
t.test(Mots ~ Age, data = eysenck, var.equal = TRUE)##
## Two Sample t-test
##
## data: Mots by Age
## t = 5.023, df = 18, p-value = 8.836e-05
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 4.247 10.353
## sample estimates:
## mean in group - mean in group +
## 19.3 12.0
## Notons que l'on fait l'hypothèse d'homogénéité des variances et donc R utilisera une estimation de la variance commune. En considérant un risque de première espèce de 5 %, on rejettrait donc l'hypothèse nulle d'absence de différence entre les deux groupes du point de vue du critère d'étude (nombre de mots rappelés). La différence de moyenne est aisée à calculer, et elle renseigne sur la direction et l'ampleur de l'effet observé sur cet échantillon. Mais il est souvent plus intéressant de reporter une mesure de taille d'effet qui tienne compte de la variabilité inter-individuelle observée dans l'échantillon.
mots.means <- with(eysenck, tapply(Mots, Age, mean))
mots.sd <- with(eysenck, tapply(Mots, Age, sd))
diff(mots.means)/mots.sd[1]## +
## -2.735diff(mots.means)/mean(mots.sd)## +
## -2.278Si l'on utilise les commandes disponibles dans le package MBESS, on obtient sensiblement les mêmes résultats, à l'exception du cas où l'on considère les deux groupes pour estimer la variance commune : dans notre cas, on a simplement calculé la moyenne des écart-types, alors que la commande smd utilise en fait l'estimation de la variance commune utilisée dans le test t, \(s_c = \sqrt{(n_1-1)s_1^2+(n_2-1)s_2^2}\big/(n_1+n_2-2)\).
library(MBESS)
with(eysenck, smd(Mots[Age == "+"], Mots[Age == "-"]))## [1] -2.246with(eysenck, smd.c(Mots[Age == "+"], Mots[Age == "-"]))## [1] -2.735Pour réaliser un test de Wilcoxon, la syntaxe est la même que pour le test t :
wilcox.test(Mots ~ Age, data = eysenck)##
## Wilcoxon rank sum test with continuity correction
##
## data: Mots by Age
## W = 95, p-value = 0.0007237
## alternative hypothesis: true location shift is not equal to 0
## On voit qu'avec une approche non-paramétrique on arriverait à la même conclusion concernant le rejet de \(H_0\).
Eysenck, M. W. (1974). Age differences in incidental learning. Developmental Psychology, 10, 936–941.