Une tâche importante dans l'analyse de données consiste à résumer les mesures collectées sur différentes unités statistiques (ou expérimentales) à l'aide de moyenne, médiane, écart-type ou autre statistiques. Cela revient égénralement à appliquer une même commande, par exemple mean, à l'ensemble des observations disponibles pour un traitement, défini comme un certain niveau d'une variable qualitative (factor) ou une combinaison de niveaux lorsque l'on considère plusieurs variables. L'approche "Split – Apply – Combine" est relativement bien documentée dans Wickham (2011), et le package plyr simplifie grandement ce genre de tâches.
Des fonctionnalités intéressantes sont également disponibles dans le package Hmisc, notamment la commande générique summary.formula que l'on peut utiliser pour résumer des relations entre variables numériques ou catégorielles exprimées sous forme de formules. Il est vivement conseillé de lire le manuel d'aide (Alzola & Harrell, 2006), qui est disponible sur le site http://biostat.mc.vanderbilt.edu/wiki/Main/Hmisc.
Voici quelques exemples d'utilisation.
library(Hmisc)
summary(low ~ ., data = birthwt, method = "reverse", overall = TRUE)##
##
## Descriptive Statistics by low
##
## +------------+-----------------+-----------------+-----------------+
## | |No |Yes |Combined |
## | |(N=130) |(N=59) |(N=189) |
## +------------+-----------------+-----------------+-----------------+
## |age | 19.0/23.0/28.0 | 19.5/22.0/25.0 | 19.0/23.0/26.0 |
## +------------+-----------------+-----------------+-----------------+
## |lwt |113.0/123.5/147.0|104.0/120.0/130.0|110.0/121.0/140.0|
## +------------+-----------------+-----------------+-----------------+
## |race : White| 56% (73) | 39% (23) | 51% (96) |
## +------------+-----------------+-----------------+-----------------+
## | Black | 12% (15) | 19% (11) | 14% (26) |
## +------------+-----------------+-----------------+-----------------+
## | Other | 32% (42) | 42% (25) | 35% (67) |
## +------------+-----------------+-----------------+-----------------+
## |smoke : Yes | 34% ( 44) | 51% ( 30) | 39% ( 74) |
## +------------+-----------------+-----------------+-----------------+
## |ptl : 0 | 91% (118) | 69% ( 41) | 84% (159) |
## +------------+-----------------+-----------------+-----------------+
## | 1 | 6% ( 8) | 27% ( 16) | 13% ( 24) |
## +------------+-----------------+-----------------+-----------------+
## | 2 | 2% ( 3) | 3% ( 2) | 3% ( 5) |
## +------------+-----------------+-----------------+-----------------+
## | 3 | 1% ( 1) | 0% ( 0) | 1% ( 1) |
## +------------+-----------------+-----------------+-----------------+
## |ht : Yes | 4% ( 5) | 12% ( 7) | 6% ( 12) |
## +------------+-----------------+-----------------+-----------------+
## |ui : Yes | 11% ( 14) | 24% ( 14) | 15% ( 28) |
## +------------+-----------------+-----------------+-----------------+
## |ftv : 0 | 49% ( 64) | 61% ( 36) | 53% (100) |
## +------------+-----------------+-----------------+-----------------+
## | 1 | 28% ( 36) | 19% ( 11) | 25% ( 47) |
## +------------+-----------------+-----------------+-----------------+
## | 2 | 18% ( 23) | 12% ( 7) | 16% ( 30) |
## +------------+-----------------+-----------------+-----------------+
## | 3 | 2% ( 3) | 7% ( 4) | 4% ( 7) |
## +------------+-----------------+-----------------+-----------------+
## | 4 | 2% ( 3) | 2% ( 1) | 2% ( 4) |
## +------------+-----------------+-----------------+-----------------+
## | 6 | 1% ( 1) | 0% ( 0) | 1% ( 1) |
## +------------+-----------------+-----------------+-----------------+
## |bwt | 2948/3267/3651 | 1928/2211/2396 | 2414/2977/3487 |
## +------------+-----------------+-----------------+-----------------+summary(bwt ~ ., data = birthwt)## bwt N=189
##
## +-------+---------+---+----+
## | | |N |bwt |
## +-------+---------+---+----+
## |low |No |130|3329|
## | |Yes | 59|2097|
## +-------+---------+---+----+
## |age |[14,20) | 51|2974|
## | |[20,24) | 56|2920|
## | |[24,27) | 36|2828|
## | |[27,45] | 46|3034|
## +-------+---------+---+----+
## |lwt |[ 80,112)| 53|2656|
## | |[112,122)| 43|3059|
## | |[122,141)| 46|3075|
## | |[141,250]| 47|3038|
## +-------+---------+---+----+
## |race |White | 96|3103|
## | |Black | 26|2720|
## | |Other | 67|2805|
## +-------+---------+---+----+
## |smoke |No |115|3056|
## | |Yes | 74|2772|
## +-------+---------+---+----+
## |ptl |0 |159|3013|
## | |1 | 24|2496|
## | |2 | 5|2767|
## | |3 | 1|3637|
## +-------+---------+---+----+
## |ht |No |177|2972|
## | |Yes | 12|2537|
## +-------+---------+---+----+
## |ui |No |161|3031|
## | |Yes | 28|2449|
## +-------+---------+---+----+
## |ftv |0 |100|2865|
## | |1 | 47|3108|
## | |2 | 30|3010|
## | |3 | 7|2522|
## | |4 | 4|3168|
## | |6 | 1|3303|
## +-------+---------+---+----+
## |Overall| |189|2945|
## +-------+---------+---+----+summary(low ~ smoke + ht + ui, data = birthwt, fun = table)## low N=189
##
## +-------+---+---+---+---+
## | | |N |No |Yes|
## +-------+---+---+---+---+
## |smoke |No |115| 86|29 |
## | |Yes| 74| 44|30 |
## +-------+---+---+---+---+
## |ht |No |177|125|52 |
## | |Yes| 12| 5| 7 |
## +-------+---+---+---+---+
## |ui |No |161|116|45 |
## | |Yes| 28| 14|14 |
## +-------+---+---+---+---+
## |Overall| |189|130|59 |
## +-------+---+---+---+---+Les résultats renvoyés ci-dessus illustrent bien la démarche générale qui consiste à définir des sous-ensembles d'observations à partir des niveaux d'un facteur ou d'une variable numérique traitée comme tel (en considérant les quartiles) et à appliquer une certaine méthode de résumé numérique de l'information : tri à plat (effectif/fréquence) lorsque la variable réponse et la variable explicative sont toutes les deux catégorielles, résumé numérique dans les autres cas. On notera également que lorsqu'une variable numérique telle que ftv présente peu de valeurs uniques (par défaut, 10), la commande summary.formula (ou summary(* ~ *)) traite cette variable comme une variable catégorielle et affiche des tableaux de fréquence plutôt qu'un résumé numérique en trois points (les trois quartiles) pour les variables numériques.
Dans des cas plus simples, comme calculer des moyennes conditionnelles ou marginales, les commandes tapply et aggregate sont généralement suffisantes. Cette dernière présente l'avantage d'accepter les formulations de type (variable réponse, variable explicative, commande) ou (variable réponse ~ variable explicative, data=, FUN=), comme on le verra dans l'exemple suivant.
Dans un premier temps, l'exercice va consister à générer des données artificielles. Comme on l'a dit lors de la deuxième séance de travaux pratiques, les simulations sont assez utiles
Supposons que l'on s'intéresse à des données publiées et pour lesquelles on dispose des moyennes, écart-types et effectifs (on n'a d'ailleurs besoin que de cela pour faire une ANOVA "à la main").
Voici une procédure basique pour générer des données artificielles pour trois groupes (k) de taille 10 (ni) de moyennes \([10, 12, 8]\) et d'écart-types \([1.2, 1.1, 1.1]\).
set.seed(101)
k <- 3
ni <- 10
mi <- c(10, 12, 8)
si <- c(1.2, 1.1, 1.1)
grp <- gl(k, ni, k * ni, labels = c("A", "B", "C"))
resp <- c(rnorm(ni, mi[1], si[1]), rnorm(ni, mi[2], si[2]), rnorm(ni, mi[3], si[3]))Une autre façon de générer les observations resp consisterait à utliser directement rnorm avec les valeurs des moyennes, mi, et d'écart-types, si. En revanche, il est ensuite néecessaire de réarranger les données car cette approche génère une succession de 3 aléas (c'est-à-dire la longueur des vecteurs de moyenne et d'écart-type).
resp <- as.vector(matrix(rnorm(ni * k, mi, si), nc = k, byrow = TRUE))Dans l'exemple ci-dessus, on appelle la commande rnorm qui retourne 30 aléas gaussiens, par lots de trois observations tirées successivement dans \(\mathcal{N}(10;1.2^2)\), \(\mathcal{N}(12;1.1^2)\), et \(\mathcal{N}(8;1.1^2)\). On arrange ces observations dans une matrice à 3 colonnes, en la remplissant avec les lots de 3 observations par ligne. Finalement, on utilise la commande as.vector sur le résultat renvoyé par matrix pour récupérer le résultat sous forme d'un vecteur, de longueur 30, avec les 10 premières valeurs correspondant à la première colonne de la matrice de résultats, donc des aléas gaussiens tirés dans \(\mathcal{N}(10;1.2^2)\), etc.
Une manière plus simple (et plus élégante) de procéder consiste à utiliser la version "multivariée" de la commande apply :
resp <- as.vector(mapply(rnorm, ni, mi, si))De manière plus générale, la commande mvrnorm du package MASS permet de générer des observations tirées dans une loi normale multivariée.
Finalement, on "assemble" les variables grp et resp dans un data.frame et on supprime ces variables de l'espace de travail.
dfrm <- data.frame(grp, resp)
rm(grp, resp)
summary(dfrm)## grp resp
## A:10 Min. : 6.39
## B:10 1st Qu.: 8.61
## C:10 Median :10.06
## Mean : 9.92
## 3rd Qu.:11.10
## Max. :13.57À partir de là, on peut calculer les moyennes de groupe, par exemple.
mi.obs <- with(dfrm, tapply(resp, grp, mean))
mi.obs## A B C
## 10.294 11.516 7.941mi.obs - mean(dfrm$resp)## A B C
## 0.377 1.599 -1.976La dernière commande affiche les écarts entre les moyennes de groupe et la moyenne générale. Une autre façon de calculer les moyennes de groupe consiste à utiliser la commande aggregate plutôt que tapply, cette commande présentant l'avantage de pouvoir travailler avec des formules, que nous utiliserons par la suite pour le modèle d'ANOVA et les représentations graphiques.
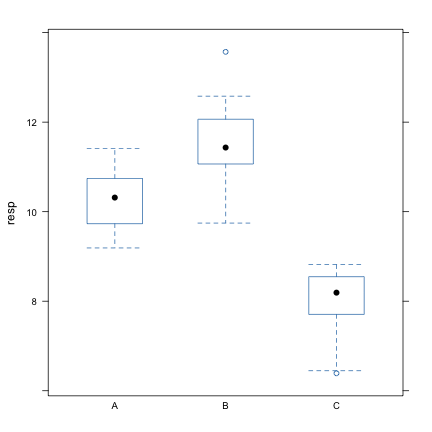
fm <- resp ~ grp
aggregate(fm, data = dfrm, FUN = mean)## grp resp
## 1 A 10.294
## 2 B 11.516
## 3 C 7.941bwplot(fm, data = dfrm)
L'ANOVA est ensuite effectuée à l'aide de la commande aov comme suit :
m1 <- aov(fm, data = dfrm)
summary(m1)## Df Sum Sq Mean Sq F value Pr(>F)
## grp 2 66.1 33.0 39.9 8.7e-09 ***
## Residuals 27 22.4 0.8
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Le résultat du test F est significatif indiquant que les données observées ne sont pas compatibles avec l'hypothèse nulle d'absence de différence entre les moyennes de groupe, en considérant un risque d'erreur de première espèce de 5 %.
Supposons maintenant que l'on ne s'intéresse qu'aux deux premiers groupes, A et B, et que l'on effectue le même modèle :
m2 <- aov(fm, data = dfrm, subset = grp == "A" | grp == "B")
summary(m2)## Df Sum Sq Mean Sq F value Pr(>F)
## grp 1 7.47 7.47 8.88 0.008 **
## Residuals 18 15.14 0.84
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1La valeur de la statistique de test, F, vaut dans ce cas 8.8794. En fait, on obtiendrait exactement les mêmes résultats en utilisant un test de Student pour échantillons indépendants, comme on peut le vérifier à partir des commandes suivantes :
dfrm2 <- subset(dfrm, subset = grp %in% c("A", "B"))
t.test(resp ~ grp, data = dfrm2, var.equal = TRUE)##
## Two Sample t-test
##
## data: resp by grp
## t = -2.98, df = 18, p-value = 0.00803
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -2.0841 -0.3605
## sample estimates:
## mean in group A mean in group B
## 10.29 11.52
## Notons que pour simplifier les choses on a créé un nouveau tableau de données restreint aux seuls groupes A et B, en utilisant une notation quelque peu différente de celle utilisée précédemment pour l'instruction subset=.
Il est possible de récupérer la valeur de la statistique de test t (ou n'importe quelle autre valeur affichée dans le tableau de résultats ci-dessus) car l'ensemble des résultats du test sont stockés dans une structure de données particulières, les list.
t.result <- t.test(resp ~ grp, data = dfrm2, var.equal = TRUE)
print(t.result$statistic^2, digits = 5)## t
## 8.8794Pour vérifier quelles sont les valeurs auxquelles on a accès, il suffit de taper
str(t.result)L'effet du tabagisme sur les performances cognitives.
Il s'agit d'une étude de Spilich, June, & Renner (1992) examinant les effets du tabagisme sur les performances. Ces auteurs ont utilisé trois tâches distinctes qui différaient par le niveau de traitement cognitif requis pour les exécuter, chaque tâche étant réalisée par des sujets différents. La première, appelée tâche d'identification d'un motif, consistait à localiser une cible sur l'écran. La deuxième, la tâche cognitive, amenait les sujets à lire un passage pour se le remémorer par la suite. La troisième était un jeu vidéo de simulation de conduite. Dans les trois cas, la variable dépendante était le nombre d'erreurs commises par le sujet (ce n'est pas exactement vrai pour toutes les tâches, mais cela permet de considérer la tâche comme une variable indépendante ; cette modification ne dénature pas les résultats de Spilich et coll.).
Les sujets ont ensuite été subdivisés en trois groupes pour ce qui est du tabagisme. Le groupe FA se composait des personnes qui fumaient de façon active pendant l'exécution de la tâche ou juste avant. Le groupe FP comprenait les sujets qui n'avaient pas fumé pendant les trois heures précédant l'exécution de la tâche (la lettre P signifie « précédemment »). Le groupe NF rassemblait les fumeurs. Les données sont disponibles dans le fichier tab13-tabagisme.dat.
Le chargement des données se fera avec la commande read.table sachant que, comme toujours, il faudra prendre garde à la manière dont les variables sont considérées par R une fois importées dans l'espace de travail. En l'occurence, la première colonne du fichier de données ne contient que des nombres (1, 2, 3) qui, sans autre action de la part de l'utilisateur, sera traitée comme une variable numérique. De plus, le fichier ne contient pas de ligne d'en-tête pour décrire les variables d'où la nécessité de le préciser à R avec l'option header=FALSE.
Dans les commandes ci-dessous, on suppose que le fichier se trouve dans le répertoire data/ qui est un sous-dossier de notre dossier de travail, qui dans le cas présent ressemble à peu près à la structure hiérarchique reproduite ci-dessous :
.
|____index.html
|____data
|____docs
|____exos
|____labs
|____slidesSachant que notre répertoire de travail actuel est labs/, on demande à R de remonter d'un cran dans la hiérarchie du système de fichiers, .., et d'aller dans le répertoire data/.
WD <- "../data"
tabac <- read.table(paste(WD, "tab13-tabagisme.dat", sep = "/"), header = FALSE)
names(tabac) <- c("Tache", "Groupe", "NErreur")
tabac$Tache <- factor(tabac$Tache, labels = c("ident", "cogn", "simul"))
summary(tabac)## Tache Groupe NErreur
## ident:45 FA:45 Min. : 0.0
## cogn :45 FP:45 1st Qu.: 6.0
## simul:45 NF:45 Median :11.0
## Mean :18.3
## 3rd Qu.:26.0
## Max. :75.0En présence de deux facteurs, il convient dans un premier temps de résumer les données séparément pour chaque variable (approche univariée). On se limitera à calculer les moyennes et écart-types par niveau des deux facteurs, en utilisant une petite fonction auxiliaire qui renvoit simplement ces quantités pour une variable quelconque.
f <- function(x) c(moy = mean(x), ety = sd(x))
aggregate(NErreur ~ Tache + Groupe, data = tabac, FUN = f)## Tache Groupe NErreur.moy NErreur.ety
## 1 ident FA 9.933 6.519
## 2 cogn FA 47.533 14.652
## 3 simul FA 2.333 2.289
## 4 ident FP 9.600 4.405
## 5 cogn FP 39.933 20.133
## 6 simul FP 6.800 5.441
## 7 ident NF 9.400 1.404
## 8 cogn NF 28.867 14.687
## 9 simul NF 9.933 6.006Pour examiner les distributions univariées, on pourra afficher des histogrammes ou des boîtes à moustaches (plus économique en terme "d'espace visuel"), sans oublier de charger le package lattice au préalable.
bwplot(NErreur ~ Tache | Groupe, data = tabac, pch = "|", layout = c(3, 1))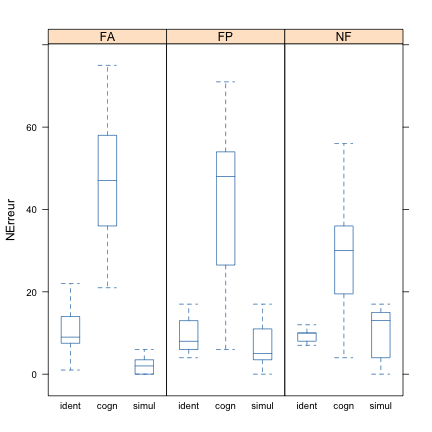
Il est également possible d'afficher les moyennes de groupes sous forme de diagramme en barres. Pour cela, il est intéressant d'exploiter le fait que la commande aggregate renvoit directement un data.frame, c'est-à-dire une structure de données que l'on peut exploiter à partir de formules comme on le fait sur un tableau de données importé avec la commande read.table.
nerreur.means <- aggregate(NErreur ~ Tache + Groupe, data = tabac, FUN = mean)
barchart(NErreur ~ Tache, data = nerreur.means, groups = Groupe, auto.key = list(column = 3))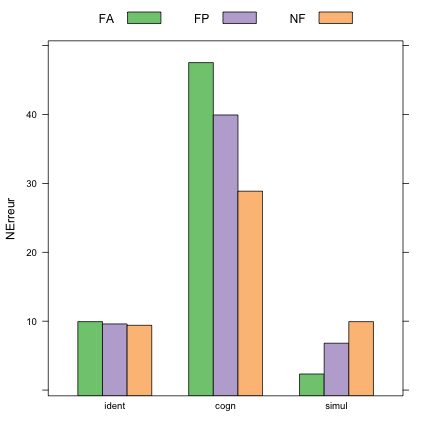
On pourra comparer ce type de représentation graphique avec des diagrammes de type dotplot de Cleveland :
dotplot(Tache ~ NErreur, data = nerreur.means, groups = Groupe, type = "l", auto.key = list(space = "right",
points = FALSE, lines = TRUE))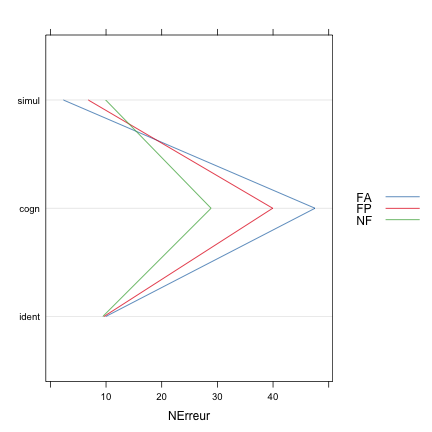
Contrairement au cas précédent, on a "renversé" la formule (Tache ~ NErreur au lieu de NErreur ~ Tache) mais ceci uniquement dans le but d'afficher Nerreur sur l'axe horizontal. Dans les deux cas, on a légèrement modifié l'affichage de la légende proposée par défaut avec l'option auto.key=TRUE. Il existe de nombreuses autres options.
À la lecture de ces graphiques, on voit clairement apparaître des tendances moyennes : les performances se dégradent dans la tâche cognitive (le nombre d'erreurs est 3 à 4 fois supérieur), et le facteur Groupe semble jouer un rôle au sein même de ces variations puisque l'on voit que le nombre d'erreurs ne varie pas dans la tâche d'identification alors que les performances moyennes semblent s'inverser dans les deux autres tâches selon que les sujets sont fumueurs (FA et FP) ou non (NF).
Concernant le modèle d'ANOVA, on considèrera le modèle complet incluant les deux effets principaux et l'interaction, ce qui revient à NErreur ~ Tache + Groupe + Tache:Groupe, ou NErreur ~ Tache * Groupe. On pourrait vérifier si le plan est équilibré en utilisant la commande replications.
aov.res <- aov(NErreur ~ Tache * Groupe, data = tabac)
summary(aov.res)## Df Sum Sq Mean Sq F value Pr(>F)
## Tache 2 28662 14331 132.90 < 2e-16 ***
## Groupe 2 355 177 1.64 0.19733
## Tache:Groupe 4 2729 682 6.33 0.00011 ***
## Residuals 126 13587 108
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1L'interaction entre les deux facteurs apparaît significative, ce qui signifie que l'on ne peut pas interpréter directement l'effet principal, également significatif, du type de tâche. On peut confirmer visuellement l'effet d'interaction à partir d'un graphique d'interaction qui révèle le non-parallélisme des segments reliant les moyennes conditionnelles :
xyplot(NErreur ~ Groupe, data = tabac, groups = Tache, type = c("a", "g"), auto.key = list(corner = c(1,
1), points = FALSE, lines = TRUE))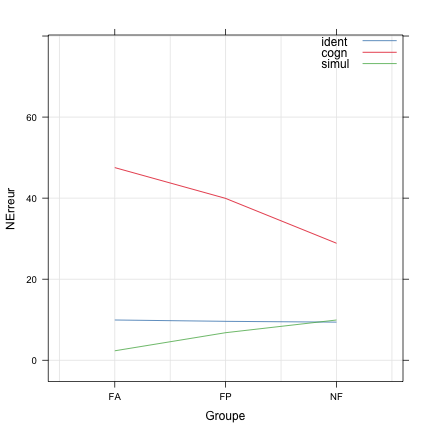
Toutefois, on peut toujours résumer les effets simples pour le facteur Tache en décomposant le tableau d'ANOVA selon les niveaux de ce facteur :
op <- options(show.signif.stars = FALSE)
for (cond in levels(tabac$Tache)) {
cat("Tâche = ", cond, "\n")
print(summary(aov(NErreur ~ Groupe, data = tabac, subset = Tache == cond)))
cat("\n")
}## Tâche = ident
## Df Sum Sq Mean Sq F value Pr(>F)
## Groupe 2 2 1.09 0.05 0.95
## Residuals 42 894 21.29
##
## Tâche = cogn
## Df Sum Sq Mean Sq F value Pr(>F)
## Groupe 2 2643 1322 4.74 0.014
## Residuals 42 11700 279
##
## Tâche = simul
## Df Sum Sq Mean Sq F value Pr(>F)
## Groupe 2 438 218.8 9.26 0.00047
## Residuals 42 993 23.6
## options(op)Dans les instructions ci-dessus, on a introduit plusieurs commandes facilitant l'affichage des résultats : la commande cat permet d'afficher n'importe quelle suite de chaînes de caractères ou de résultats R, suivie éventuellement d'un passage à la ligne (\n). Les différents modèles d'ANOVA ont été estimés pour chaque niveau du facteur Tache, d'où les itérations sur les labels de ce facteur (levels(tabac$Tache)). Enfin, pour faciliter la lecture, on a supprimé l'affichage des symboles de significativité apparaissant en bas des tableaux d'ANOVA produits par la commande summary.aov.
Ces résultats permettent donc de confirmer les observations précédentes : bien que l'effet du facteur Groupe ne soit pas significatif lorsque l'on considère l'ensemble de ses niveaux, on retrouve un effet du tabagisme dans les tâche cognitive et de simulation, ce qui apparaît plus clairement dans le graphique d'interaction suivant (on a juste interverti le facteur de groupement) :
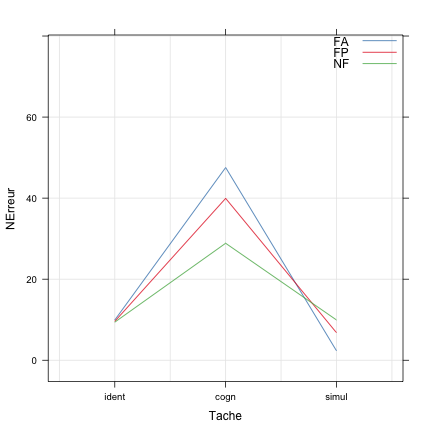
Néanmoins il ne faut pas perdre de vue que cette comparaison un par un est moins puissante par rapport à l'analyse à deux facteurs notamment car elle est basée sur un échantillon plus réduit et que on accumule l'erreur sans correction comme pour une comparaison multiple non protégée.
Bien que l'on ne montre pas comment vérifier les conditions d'application des tests F utilisés ci-dessus, les éléments de réponse ont été fournis dans le cours n°3 : l'inspection des distributions univariées (en considérant les croisement de tous les niveaux des deux facteurs), éventuellement associée à un test formel tel que celui fourni par la commande bartlett.test, permettra de vérifier si l'hypothèse d'homogénéité des variances est réaliste ; la normalité des résidus pourra être évaluée à l'aide de diagramme en quantile (qqmath). Quant à l'indépendance, elle découle naturellement de l'organisation même du plan d'expérience.
On pourrait se demander quelle est la part de variance expliquée par le modèle complet (qui revient à une mesure globale de taille d'effet), ou en d'autres termes la part de variabilité dans le nombre d'erreurs observée dont les facteurs d'étude sont susceptibles de rendre compte : contrairement à l'ANOVA à un seul facteur, où il s'agit simplement du rapport entre la somme des carrés du facteur et la somme des carrés totale (facteur + résiduelle), en présence de plusieurs facteurs on peut décomposer cette "variance expliquée" en effets partiels, notés \(\eta^2_{\text{partiel}}\). Il est donc possible de calculer tous ces effets partiels à partir du premier tableau d'ANOVA. Par exemple, pour le facteur Tache, l'effet partiel est estimé comme suit :
28662/(28662 + 13587)## [1] 0.6784soit environ 68 % de variance expliquée.
Il est également possible d'associer des intervalles de confiance à ces statistiques, à l'aide de la commande ci.pvalf du package MBESS. Voir le site http://yatani.jp/HCIstats/ANOVA pour des exemples d'utilisation.
Alzola, C., & Harrell, F. (2006). An Introduction to S and The Hmisc and Design Libraries. Retrieved from http://biostat.mc.vanderbilt.edu/wiki/pub/Main/RS/sintro.pdf
Spilich, G. J., June, L., & Renner, J. (1992). Cigarette smoking and cognitive performance. Bristish Journal of Addiction, 87, 1313–1326.
Wickham, H. (2011). The Split-Apply-Combine Strategy for Data Analysis. Journal of Statistical Software, 40.