Les commandes de base pour travailler avec des mesures d'association entre deux variables numériques (corrélation) sont cor et cor.test, cette dernière fournissant à la fois un intervalle de confiance à \(1-\alpha\) et un test pour l'hypothèse nulle \(\rho=0\). L'option method="spearman" donne accès au coefficient de corrélation basé sur les rangs des observations. Dans le cas où il y a des valeurs manquantes (inégalement réparties sur les deux séries de mesure), il est nécessaire de demander à R de calculer la corrélation sur les paires d'observations "complètes", grâce à l'option use="pairwise.complete.obs" (ou use="pair" puisqu'il est possible d'abréger le nom des options lorsque cela ne prête pas à confusion).
Avant de calculer un coefficient de corrélation, il est toujours préférable de visualiser les données à l'aide d'un simple diagramme de dispersion. Une approche de type "loess" permet souvent de se faire une idée sur la linéarité de la relation entre les deux variables (Cleveland, 1979).
La commande xyplot permet de représenter la relation entre deux variables sous forme de diagramme de dispersion. Pour illustrer son usage, considérons les données suivantes (Moore & McCabe, 2006).
Smoking and Cancer.
Government statisticians in England conducted a study of the relationship between smoking and lung cancer. The data concern 25 occupational groups and are condensed from data on thousands of individual men. The explanatory variable is the number of cigarettes smoked per day by men in each occupation relative to the number smoked by all men of the same age. This smoking ratio is 100 if men in an occupation are exactly average in their smoking, it is below 100 if they smoke less than average, and above 100 if they smoke more than average. The response variable is the standardized mortality ratio for deaths from lung cancer. It is also measured relative to the entire population of men of the same ages as those studied, and is greater or less than 100 when there are more or fewer deaths from lung cancer than would be expected based on the experience of all English men.
(Source: http://lib.stat.cmu.edu/DASL/Stories/SmokingandCancer.html)
Le chargement des données se fera manuellement, comme suit :
smoking <- c(77, 137, 117, 94, 116, 102, 111, 93, 88, 102, 91, 104, 107, 112, 113,
110, 125, 133, 115, 105, 87, 91, 100, 76, 66)
mortality <- c(84, 116, 123, 128, 155, 101, 118, 113, 104, 88, 104, 129, 86, 96,
144, 139, 113, 146, 128, 115, 79, 85, 120, 60, 51)
d <- data.frame(smoking, mortality)
rm(smoking, mortality)
summary(d)## smoking mortality
## Min. : 66 Min. : 51
## 1st Qu.: 91 1st Qu.: 88
## Median :104 Median :113
## Mean :103 Mean :109
## 3rd Qu.:113 3rd Qu.:128
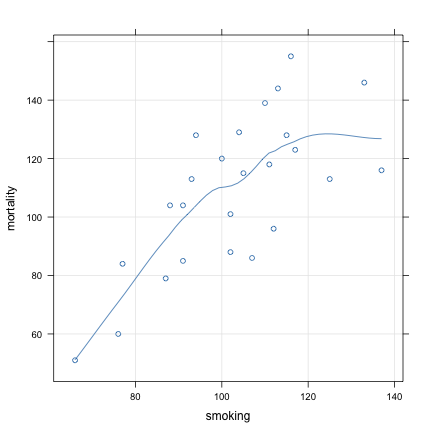
## Max. :137 Max. :155xyplot(mortality ~ smoking, data = d, type = c("p", "g", "smooth"))
L'option type=c("p","g","smooth") permet d'afficher les données sous forme de points, ainsi qu'une grille facilitant la lecture des axes et une droite de régression "loess" dont le paramètre de lissage peut être contrôlé avec l'option span=. Par exemple,
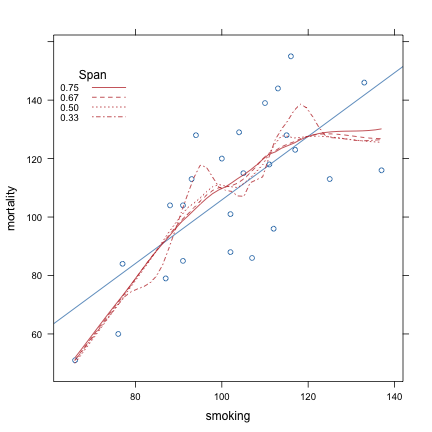
xyplot(mortality ~ smoking, data = d, type = c("p", "g", "smooth"), span = 1/3)produira une courbe "moins lisse" car la régression locale sera beaucoup sensible aux variations locales (en raison de la taille de la fenêtre de lissage). Voici quelques variations du paramètre span et son effet sur le degré de lissage de la courbe. On a également rajouté la droite de régression à l'aide de l'option type="r".
spans <- rev(c(1/3, 1/2, 2/3, 3/4))
my.key <- list(x = 0, y = 0.75, corner = c(0, 0), title = "Span", cex.title = 1,
text = list(format(spans, digits = 2), cex = 0.8), lines = list(type = "l", lty = 1:length(spans),
col = "#BF3030"))
xyplot(mortality ~ smoking, data = d, type = c("p", "r"), key = my.key, panel = function(x,
y, ...) {
panel.xyplot(x, y, ...)
for (sp in seq_along(spans)) panel.loess(x, y, span = spans[sp], col = "#BF3030",
lty = sp, ...)
})
Le coefficient de corrélation de Bravais-Pearson est obtenu ainsi :
with(d, cor(mortality, smoking))## [1] 0.7162La corrélation entre les deux variables est donc positive et d'amplitude relativement élevée. On rejeterait d'ailleurs l'hypothèse nulle d'absence de corrélation linéaire entre ces deux variables.
cor.test(~mortality + smoking, data = d)##
## Pearson's product-moment correlation
##
## data: mortality and smoking
## t = 4.922, df = 23, p-value = 5.658e-05
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.4479 0.8662
## sample estimates:
## cor
## 0.7162
## Notons que si l'on souhaite tester une hypothèse nulle différente, par exemple \(H_0:\rho=0.300\), il est nécessaire d'utiliser un autre type de commande. Par exemple,
library(psych)
r.test(nrow(d), 0.3, 0.716)## Correlation tests
## Call:r.test(n = nrow(d), r12 = 0.3, r34 = 0.716)
## Test of difference between two independent correlations
## z value 1.96 with probability 0.05Enfin, si l'on souhaite une mesure non-paramétrique de l'association, on utilisera plutôt
with(d, cor(mortality, smoking, method = "spearman"))## [1] 0.6932Pour l'essentiel, la commande lm se charge de construire le modèle de régression et plusieurs autres commandes permettent de travailler à partir du résultat renvoyé par lm (comme pour aov). On retiendra essentiellement les commandes summary pour afficher un tableau avec les coefficients de régression et leurs tests t associés (attention au codage des contrastes pour l'interprétation avec des données qualitatives) et anova pour afficher un tableau d'ANOVA de la régression. Les extracteurs resid et fitted sont utiles pour obtenir les résidus et les valeurs prédites par le modèle, à partir des données observées (autrement, voir la commande predict).
Avec les données précédentes, le modèle de régression liénaire simple s'obtient ainsi :
m <- lm(mortality ~ smoking, data = d)
summary(m)##
## Call:
## lm(formula = mortality ~ smoking, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -30.11 -17.89 3.15 14.13 31.73
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.885 23.034 -0.13 0.9
## smoking 1.088 0.221 4.92 5.7e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 18.6 on 23 degrees of freedom
## Multiple R-squared: 0.513, Adjusted R-squared: 0.492
## F-statistic: 24.2 on 1 and 23 DF, p-value: 5.66e-05
## Le test global sur la régression est significatif (F=24.2) et c'est le même que l'on retrouvera dans le tableau d'ANOVA plus bas. Le coefficient de régression pour la pente vaut 1.0888, indiquant que lorsque le rapport de consommation de tabac augmente d'une unité le taux de mortalité standardisé varie d'environ 1.1 unité. On peut retrouver les coefficients de régression de la manière suivante :
coef(m)## (Intercept) smoking
## -2.885 1.088Pour obtenir leurs intervalles de confiance à 95 %, on utilisera la commande confint :
confint(m)## 2.5 % 97.5 %
## (Intercept) -50.5342 44.764
## smoking 0.6305 1.545Comme on peut le voir, l'intervalle de confiance pour la pente ne contient pas la valeur 0 et on concluera de la manière sur la significativité de la relation linéaire et de l'association positive entre la consommation de tabac et le taux de mortalité.
Le tableau d'ANOVA est rarement utile dans le cas où il n'y a qu'une variable explicative (régression linéaire simple) puisque l'essentiel de l'information est déjà fournie par summary(m). Toutefois, cela peut être utile dans le cas où il y a plusieurs variables explicative, ou en présence de variables catégorielles.
anova(m)## Analysis of Variance Table
##
## Response: mortality
## Df Sum Sq Mean Sq F value Pr(>F)
## smoking 1 8396 8396 24.2 5.7e-05 ***
## Residuals 23 7970 347
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1La qualité d'ajustement du modèle peut être vérifiée à partir du coefficient de détermination qui est affichée par summary(m) et qui vaut ici 0.513. Il s'interprète comme la part de variance expliquée par la régression ; il s'agit en fait de la corrélation entre les valeurs prédites et les valeurs observées :
cor(fitted(m), d$mortality)^2## [1] 0.513(Dans le cas multivarié, il faudra plutôt prendre en compte le coefficient ajusté qui tient compte du nombre de paramètres dans le modèle.)
L'essentiel de l'activité de diagnostic du modèle (mauvaise spécification et points influents) repose sur l'analyse des résidus, ceux-ci étant accessibles à partir de la commande resid. En particulier, l'examen de la distribution des résidus en fonction des valeurs prédites ou observées permettra de vérifier les éventuels écarts par rapport aux hypothèses de linéarité et de constance de la variance.
library(gridExtra)
p1 <- xyplot(resid(m) ~ smoking, data = d, abline = list(h = 0))
p2 <- xyplot(resid(m) ~ fitted(m), abline = list(h = 0))
grid.arrange(p1, p2, nrow = 1)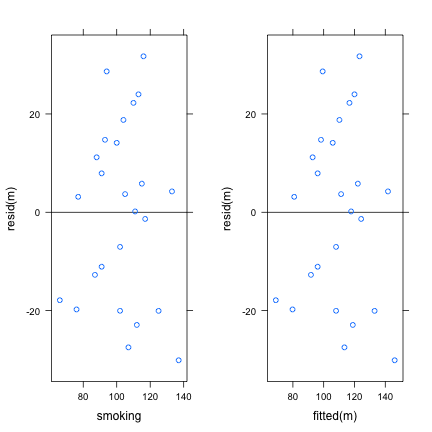
Quant à l'influence des observations dans la stabilité des coefficients du modèle, la commande essentielle est
m.inf <- influence.measures(m)
head(m.inf$infmat)## dfb.1_ dfb.smkn dffit cov.r cook.d hat
## 1 0.06408 -0.058680 0.07002 1.2590 0.002559 0.13435
## 2 0.78839 -0.869204 -0.96943 1.0088 0.421068 0.20400
## 3 0.01017 -0.012813 -0.01995 1.1722 0.000208 0.06809
## 4 0.22912 -0.177125 0.37993 0.9153 0.067260 0.05111
## 5 -0.23245 0.298295 0.48555 0.8739 0.106599 0.06425
## 6 -0.01649 0.004039 -0.07745 1.1239 0.003116 0.04011On peut distinguer différents types de points influents :
La fonction resid permet d'obtenir les résidus "simples", \(e_i=y_i-\hat y_i\), de variance non-constante, mais on montre que celle-ci est fonction de \(\sigma_{\varepsilon}^2\) : \[\text{Var}(e_i)=\sigma_{\varepsilon}^2(1-h_i),\] où \(h_i\) ("hat value") est l'effet levier de la \(i\)ème observation sur l'ensemble des valeurs ajustées via le modèle de régression. Les points exerçant un fort effet levier tendent donc à avoir de plus faibles résidus (puisqu'ils "tirent" la droite de régression vers eux).
Voir Influence Diagnostics ou Fox & Weisberg (2011) pour une description précise des différents indices d'influence des observations.
Cleveland, W. S. (1979). Robust locally weighted regression and smoothing scatterplots. Journal of the American Statistical Association, 74, 829–836.
Fox, J., & Weisberg, S. (2011). An R companion to Applied Regression. Sage.
Moore, D. S., & McCabe, G. P. (2006). Introduction to the Practice of Statistics. W.H. Freeman & Company.