On s'intéressera dans cette séance aux comparaisons multiples de moyennes (prévues avant l'expérience ou mises en oeuvre après avoir observé les résultats, donc post-hoc), et à la modélisation de données présentant une structure de corrélation intra-unité résultant d'un plan d'expérience spécifique où plusieurs mesures sont recueillies sur la même unité statistique. Ce dernier point rend l'approche de modélisation différente des problèmes abordés jusqu'à présent puisque l'on travaillait avec des groupes indépendants, hypothèse d'indépendance que l'on retrouvait au niveau de la distribution supposée pour les résidus des modèles. Qui plus est, l'introduction d'un facteur sujet dans le plan d'analyse pose la question du choix de sa formulation dans le modèle d'ANOVA, c'est-à-dire sous la forme d'un effet fixe ou aléatoire, la dernière option étant souvent la plus intéressante car elle permet de généraliser les résultats observés à la population cible (dans laquelle les sujets ont été échantillonnés).
On va s'intéresser à deux approches de comparaisons multiples de moyennes, l'exercice étant largement inspiré de Howell (1998).
Après avoir réalisé une ANOVA à un facteur et vérifié la significtaivité de l'effet principal, on utilisera deux techniques de comparaisons multiples de moyenne – contrastes et tests post-hoc de Tukey – même si l'étude qui nous servira de support et qui est décrite ci-après suggère clairement que seule la première approche est réellement justifiée puisque les hypothèses sont définies a priori.
Tolérance à la morphine.
Il s'agit d'une étude hypothétique similaire à une expérience importante réalisée par Siegel (1975) sur la tolérance à la morphine. Les données sont fictives et la description des conditions est « allégée », mais les moyennes (et le degré de signification des différences entre les moyennes) sont les mêmes que celles de l'article de Siegel. La morphine est un médicament souvent utilisé pour atténuer la douleur. Cependant, des administrations répétées de morphine provoquent un phénomène de tolérance : la morphine a de moins en moins d'effet (la réduction de la douleur est de moins en moins forte) au fil du temps. Pour mettre en évidence la tolérance à la morphine, on a souvent recours à une expérience qui consiste à placer un rat sur une surface trop chaude. Lorsque la chaleur devient trop insupportable, le rat va se mettre à se lécher les pattes ; le temps de latence qui précède le moment où le rat commence à se lécher les pattes est utilisé comme mesure de sa sensibilité à la douleur. Un rat qui vient de recevoir une injection de morphine montre en général un temps de latence plus long, ce qui montre que sa sensibilité à la douleur est réduite. Le développement de la tolérance à la morphine est indiqué par le fait que les latences se raccourcissent progressivement (signe d'une sensibilité accrue) sous l'effet des injections répétées de morphine.
Siegel a constaté que dans plusieurs situations impliquant des médicaments autres que la morphine, les réponses conditionnées (apprises) au médicament vont en sens inverse des effets inconditionnés (naturels) du médicament. Par exemple, un animal à qui l'on a injecté de l'atropine a tendance à manifester une diminution prononcée de la salivation. Par contre, si, après des injections répétées d'atropine, on administre soudain, dans le même environnement physique, une solution saline (qui ne devrait avoir absolument aucun effet), la salivation de l'animal va augmenter. C'est comme si celui-ci compensait l'effet anticipé de l'atropine. Dans ce type d'étude, il semble qu'un mécanisme compensatoire appris se développe au fil des essais pour contrebalancer l'effet du médicament.
Siegel a formulé la théorie selon laquelle ce processus pourrait contribuer à expliquer la tolérance à la morphine. D'après son raisonnement, si, durant une série d'essais préliminaires, on injecte de la morphine à l'animal placé sur une surface chaude, une certaine tolérance à la morphine va se développer. Donc, si le sujet reçoit une nouvelle injection de morphine lors d'un test ultérieur, il sera aussi sensible à la douleur que le serait un animal naïf (c'est-à-dire qui n'a jamais reçu d'injection de morphine). Siegel poursuit son raisonnement : si, lors du test, on injecte plutôt à l'animal une solution saline physiologique dans le même environnement physique, l'hypersensibilité conditionnée résultant de l'administration répétée de morphine ne sera pas contrebalancée par la présence de morphine et l'animal manifestera des temps de latence très courts avant de se lécher les pattes. En outre, selon Siegel, si l'on administre des injections répétées de morphine dans un environnement avant de le tester dans un environnement différent, le nouvel environnement ne suscitera pas l'hypersensibilité compensatoire conditionnée pour contrebalancer la morphine. En conséquence, le sujet réagira comme le ferait un animal qui reçoit sa toute première injection. L'héroïne est un dérivé de la morphine. Imaginons un héroïnomane qui consomme de fortes doses en raison du développement d'un phénomène de tolérance. Si sa réaction à cette forte dose devient subitement celle d'une personne qui n'a jamais consommé de drogue, au lieu d'être celle d'un habitué, le résultat pourrait s'avérer mortel ; c'est d'ailleurs souvent le cas. Il s'agit alors d'un problème très grave.
L'une des versions de l'expérience de Siegel se base sur la prédiction qui vient d'être esquissée. L'expérience implique cinq groupes de rats. Chaque groupe participe à quatre essais, mais les données d'analyse sont uniquement prélevées lors du dernier essai critique (test). On désigne les groupes en indiquant le traitement appliqué lors des trois premiers essais puis du quatrième. Le groupe M-M a reçu des injections de morphine lors des trois premiers essais dans l'environnement de test, puis de nouveau ors du quatrième essai, dans le même environnement. Il s'agit du groupe standard en ce qui concerne la tolérance à la morphine, et l'on s'attend à y relever des niveaux normaux de sensibilité à la douleur. Le groupe M-S a reçu une injection de morphine (dans l'environnement de test) lors des trois premiers essais puis une solution saline lors du quatrième. On s'attend à ce que ces animaux se caractérisent par une hypersensibilité à la douleur puisque l'hypersensibilité conditionnée ne sera pas contrebalancée par les effets compensatoires de la morphine. Les animaux du groupe M(cage)-M (en abrégé, Mc-M) ont reçu une injection de morphine lors des trois premiers essais, effectués dans leur cage habituelle, puis la même injection lors du quatrième essai, mais dans l'environnement de test standard, qu'ils ne connaissaient pas. Dans ce groupe, les indices initialement associés à l'injection de morphine n'étaient pas présents lors du test ; on ne devrait donc pas s'attendre à constater, chez ces animaux, une tolérance à la morphine lors du test. Le quatrième groupe (le groupe S-M) a reçu une injection de solution saline durant les trois premiers essais (dans l'environnement de test) et de morphine lors du quatrième. On s'attend à ce que ces animaux manifestent la sensibilité la plus réduite à la douleur puisqu'ils n'ont eu aucune occasion de développer une certaine tolérance à la morphine. Enfin, le groupe S-S a reçu une injection de solution saline lors des quatre essais. Si Siegel a raison, c'est le groupe S-M qui devrait présenter les temps de latence les plus longs (indiquant une sensibilité minimale) et le groupe M-S les temps de latence les plus courts (sensibilité maximale). Le groupe Mc-M devrait se rapprocher du groupe S-M puisque les indices associés aux trois premiers essais du groupe Mc-M ne sont pas présents lors du test. Les groupes M-M et S-S devraient se situer à un niveau intermédiaire. L'égalité ou non des groupes M-M et S-S dépendra de la vitesse à laquelle se développe la tolérance à la morphine. Le schéma des résultats ainsi anticipés est le suivant :
S-M = Mc-M > M-M ? S-S > M-SLe point d'interrogation indique l'absence de prédiction. La variable dépendante est le temps de latence (en secondes) qui s'écoule avant que l'animal ne commence à se lécher les pattes.
Les données sont disponibles dans le fichier texte tab12-1.dat. En supposant que le fichier soit dans le répertoire ../data (si ce n'est pas le cas, modifier le chemin d'accès au fichier), on charge les données de la manière suivante :
d <- read.table("../data/tab12-1.dat", header = FALSE)[-1]
names(d) <- c("Groupe", "Latence")
d$Groupe <- factor(d$Groupe, levels = 1:5, labels = c("M-S", "M-M", "S-S", "S-M",
"Mc-M"))
summary(d)## Groupe Latence
## M-S :8 Min. : 1.0
## M-M :8 1st Qu.: 6.0
## S-S :8 Median :13.5
## S-M :8 Mean :15.6
## Mc-M:8 3rd Qu.:24.2
## Max. :40.0La première colonne dans le fichier tab12-1.dat représente en fait le code sujet dont on n'a pas vraiment besoin dans cet exercice, d'où sa suppression lors du chargement des données.
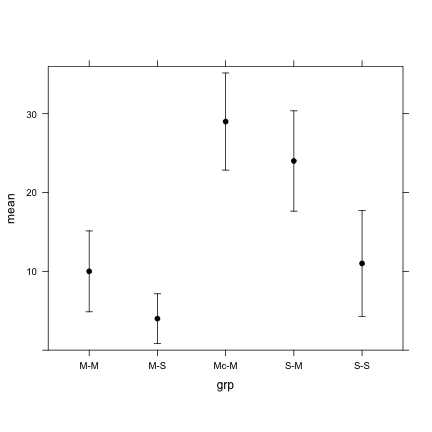
On profitera de ce qui a été vu dans les applications précédentes pour produire les graphiques descriptifs appropriés (p. ex., boîtes à moustaches pour décrire les distributions individuelles par groupe) et vérifier numériquement les moyennes et variances intra-groupe. Par exemple, voici la distribution des moyennes (\(\pm 1\) écart-type, à titre descriptif) :
mm <- with(d, tapply(Latence, Groupe, mean))
ss <- with(d, tapply(Latence, Groupe, sd))
dm <- data.frame(grp = levels(d$Groupe), mean = mm, lwr = mm - ss, upr = mm + ss)
xyplot(mean ~ grp, data = dm, lwr = dm$lwr, upr = dm$upr, type = "p", ylim = c(0,
36), col = "black", pch = 19, aspect = 0.8, panel = function(x, y, lwr, upr,
...) {
panel.xyplot(x, y, ...)
panel.arrows(x, lwr, x, upr, angle = 90, code = 3, length = 0.05)
})
Notons que la commande xYplot dans le package Hmisc est beaucoup plus commode pour ce genre de graphiques. Plutôt que d'utiliser des écart-types, on aurait pu représenter des intervalles de confiance à 95 % (pour avoir une idée de la précision de l'estimation de ces moyennes à partir des échantillons aléatoires) ou les erreur-types (p. ex., 1.96\(s_i/\sqrt{n}\)).
Le modèle d'ANOVA à un facteur ne pose pas de difficulté particulière :
m <- aov(Latence ~ Groupe, data = d)
summary(m)## Df Sum Sq Mean Sq F value Pr(>F)
## Groupe 4 3498 874 27.3 2.4e-10 ***
## Residuals 35 1120 32
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1model.tables(m)## Tables of effects
##
## Groupe
## Groupe
## M-S M-M S-S S-M Mc-M
## -11.6 -5.6 -4.6 8.4 13.4et on peut vérifier que l'effet du facteur principal (Groupe) est hautement significatif (env. 76 % de variance expliquée). Ce test F indique qu'au moins une paire de moyennes est significativement différente (de manière équivalente, \(\mu_i-\mu_j\neq 0\)) et l'objet du reste des analyses est de voir (1) si des hypothèses spécifiées à l'avance peuvent être confirmées à partir des données observées, et (2) sans a priori sur les traitement possiblement différent, tester l'ensemble des 10 paires de moyennes.
Pour préciser la contribution de chaque groupe dans les différences globales détectées par l'ANOVA, une première approche consisterait à comparer toutes les paires de moyennes à l'aide de tests t dits "protégés" (méthode de Bonferroni), encore appelé test de Dunn.
with(d, pairwise.t.test(Latence, Groupe, p.adjust.method = "bonf"))##
## Pairwise comparisons using t tests with pooled SD
##
## data: Latence and Groupe
##
## M-S M-M S-S S-M
## M-M 0.41051 - - -
## S-S 0.18319 1.00000 - -
## S-M 3.1e-07 0.00019 0.00054 -
## Mc-M 1.9e-09 8.9e-07 2.6e-06 0.85818
##
## P value adjustment method: bonferroniDe ces résultats on en conclue que seuls peuvent être considérés comme significativement différents les groupes M-S et S-M, M-S et Mc-M, M-M et S-M, M-M et Mc-M, et enfin S-S et Mc-M. À la lecture de ces résultats, on se retrouve bien avec 2 "paquets" de moyennes : les groupes M-S, M-M et S-S vs. les groupes S-M et Mc-M. Il n'y a pas de différences entre les groupes pour un même paquet, mais les paquets diffèrent entre eux.
Une autre approche est d'utiliser des tests HSD de Tukey puisque les groupes sont équilibrés. Voici le résultat de ces tests pour le modèle d'ANOVA considéré plus haut :
hsd <- TukeyHSD(m)
hsd## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = Latence ~ Groupe, data = d)
##
## $Groupe
## diff lwr upr p adj
## M-M-M-S 6 -2.132 14.132 0.2340
## S-S-M-S 7 -1.132 15.132 0.1198
## S-M-M-S 20 11.868 28.132 0.0000
## Mc-M-M-S 25 16.868 33.132 0.0000
## S-S-M-M 1 -7.132 9.132 0.9965
## S-M-M-M 14 5.868 22.132 0.0002
## Mc-M-M-M 19 10.868 27.132 0.0000
## S-M-S-S 13 4.868 21.132 0.0005
## Mc-M-S-S 18 9.868 26.132 0.0000
## Mc-M-S-M 5 -3.132 13.132 0.4078
## Il est également possible de visualiser graphiquement les résultats (différence de moyennes et intervalle de confiance associé).
plot(hsd)
Comme des hypothèses spécifiques sont clairement formulées dans l'énoncé du problème, il est légitime d'utiliser des contrastes pour tester spécifiquement certaines combinaisons linéaires des moyennes de groupe.
Utilisation de simples contrastes linéaires. Il s'agit de combinaisons linéaires de moyennes, du type \(\sum_i\alpha_i\bar x_i\) (comme dans le cas des contrastes orthogonaux), qui qui ne sont pas indépendantes. Supposons que l'on ait prévu, avant l'expérience, de comparer
Il y a donc 4 comparaisons à effectuer, et les contrastes peuvent être résumés dans une matrice de contraste comme suit : (attention les contrastes sont en lignes et non en colonnes comme dans les commandes R pour les contrastes) :
cont <- rbind(c(-3, 2, -3, 2, 2), c(0, -1, 0, 0, 1), c(-1, 0, 1, 0, 0), c(0, 1, -1,
0, 0))
cont## [,1] [,2] [,3] [,4] [,5]
## [1,] -3 2 -3 2 2
## [2,] 0 -1 0 0 1
## [3,] -1 0 1 0 0
## [4,] 0 1 -1 0 0Pour tester chacun de ces contrastes, on utilisera le package multcomp (à installer si ce n'est pas déjà fait : install.packages("multcomp")) et la commande glht :
library(multcomp)
r <- glht(aov(Latence ~ Groupe, data = d), linfct = mcp(Groupe = cont))
summary(r)##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: User-defined Contrasts
##
##
## Fit: aov(formula = Latence ~ Groupe, data = d)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## 1 == 0 81.00 10.95 7.39 <0.001 ***
## 2 == 0 19.00 2.83 6.72 <0.001 ***
## 3 == 0 7.00 2.83 2.47 0.063 .
## 4 == 0 -1.00 2.83 -0.35 0.985
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)
## A titre indicatif, on peut recalculer le premier contraste (\(c_1\)) manuellement. Pour cela, il faut calculer la SC associée à ce contraste. Celle-ci vaut simplement \[\text{SC}_1=\frac{n\left(\sum\alpha_i\bar x_i)\right)^2}{\sum\alpha_i^2},\] où \(\alpha_i=[-3; 2; -3; 2; 2]\). Sous R, cela donne :
a.mean <- with(d, tapply(Latence, Groupe, mean))
c1 <- sum(cont[1, ] * a.mean)
SC1 <- (8 * c1^2)/sum(cont[1, ]^2)Le CM associé à ce contraste est égal à la SC car il n'y a qu"un degré de liberté (on compare deux groupes, soit deux moyennes). Pour obtenir la valeur F associée à cette comparaison, il suffit donc de diviser la valeur de la SC calculée par le CM de l'erreur. Celui-ci vaut 32 comme l'indique l'examen de la table d'ANOVA présentée plus haut. On a donc
(F1 <- SC1/32)## [1] 54.67qf(0.95, 1, 35)## [1] 4.121La valeur F calculée étant largement supérieure à la valeur repère d'une distribution de Fisher-Snedecor à 1 et 35 ddl, on en conclut que les groupes M-S et S-S diffèrent en moyenne des groupes M-M, S-M et Mc-M réunis. On pourrait en profiter pour vérifier qu’un test t donnerait exactement le même résultat (pour les comparaisons à 1 ddl, \(F = t^2\)). Il faudrait pour cela effectuer un test t en utilisant comme variance commune la variance résiduelle, c'est-à-dire la moyenne des variances intra-groupe. Pour le contraste \(c_2\), qui permet de comparer le groupe M-M au groupe Mc-M, on aurait avec un test t classique :
d.t.test <- with(d, t.test(Latence[as.numeric(Groupe) == 2], Latence[as.numeric(Groupe) ==
5], var.equal = TRUE))
d.t.test##
## Two Sample t-test
##
## data: Latence[as.numeric(Groupe) == 2] and Latence[as.numeric(Groupe) == 5]
## t = -6.703, df = 14, p-value = 1.006e-05
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -25.08 -12.92
## sample estimates:
## mean of x mean of y
## 10 29
## La valeur de F vaut quant à elle :
c2 <- sum(cont[2, ] * a.mean)
SC2 <- (8 * c2^2)/sum(cont[2, ]^2)
SC2/32## [1] 45.12à comparer à
d.t.test$statistic^2## t
## 44.92La différence s'explique par le fait que pour le test t, la variance commune utilisée ne tient compte que des deux groupes comparés (moyenne des variances de M-M et Mc-M), alors que pour le contraste la variance commune est estimée à partir de tous les groupes : ceci est légitime dans la mesure où on a considéré que les variances étaient homogènes pour valider le résultat du test d’ANOVA. On gagne donc à estimer la variance résiduelle avec le maximum d’information (sur les groupes).
Utilisation de contrastes orthogonaux. Les comparaisons précédentes ne sont pas indépendantes et il serait possible de considérer un seuil de significativité plus bas (par exemple, 0.01) pour maintenir un taux d'erreur d'ensemble (FWER) inférieur ou égal à 5 %, ou simplement de corriger le risque de première espèce nominal comme on l'a fait plus haut (cf. Adjusted p values reported -- single-step method dans la sortie produite par glht). Une solution alternative est d'utiliser des contrastes orthogonaux, comme Howell (p. 409) qui propose la matrice de contrastes suivante :
cont2 <- rbind(c(3, 3, -2, -2, -2), c(1, -1, 0, 0, 0), c(0, 0, 2, -1, -1), c(0, 0,
0, 1, -1))
cont2## [,1] [,2] [,3] [,4] [,5]
## [1,] 3 3 -2 -2 -2
## [2,] 1 -1 0 0 0
## [3,] 0 0 2 -1 -1
## [4,] 0 0 0 1 -1apply(cont2, 1, sum) # somme à zéro## [1] 0 0 0 0crossprod(t(cont2)) # produit vectoriel nul (hors-daigonal)## [,1] [,2] [,3] [,4]
## [1,] 30 0 0 0
## [2,] 0 2 0 0
## [3,] 0 0 6 0
## [4,] 0 0 0 2On peut visualiser le partitionnement de la SC liée au traitement sous forme schématique :
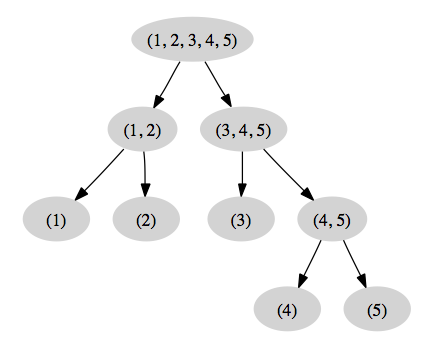
D'où les tests suivants, toujours avec la commande glht :
r2 <- glht(aov(Latence ~ Groupe, data = d), linfct = mcp(Groupe = cont2))
summary(r2)##
## Simultaneous Tests for General Linear Hypotheses
##
## Multiple Comparisons of Means: User-defined Contrasts
##
##
## Fit: aov(formula = Latence ~ Groupe, data = d)
##
## Linear Hypotheses:
## Estimate Std. Error t value Pr(>|t|)
## 1 == 0 -86.00 10.95 -7.85 <1e-04 ***
## 2 == 0 -6.00 2.83 -2.12 0.15
## 3 == 0 -31.00 4.90 -6.33 <1e-04 ***
## 4 == 0 -5.00 2.83 -1.77 0.29
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)
## On en conclut que les trois premiers contrastes sont significatifs à 5 %, mais on ne met en évidence aucune différence entre les traitements S-M et Mc-M.
L'exemple servant de support pour l'application numérique est tiré de Vittinghoff, Glidden, Shiboski, & McCulloch (2005).
Enzymes digestives et excès de graisse.
Lack of digestive enzymes in the intestine can cause bowel absorption problems, as indicated by excess fat in the feces. Pancreatic enzyme supplements can be given to ameliorate the problem.
Les données sont construites de la manière suivante.
fat <- data.frame(fecfat = c(44.5, 33, 19.1, 9.4, 71.3, 51.2, 7.3, 21, 5, 4.6, 23.3,
38, 3.4, 23.1, 11.8, 4.6, 25.6, 36, 12.4, 25.4, 22, 5.8, 68.2, 52.6), pilltype = gl(4,
6, labels = c("None", "Tablet", "Capsule", "Coated")), subject = gl(6, 1))
head(fat, n = 10)## fecfat pilltype subject
## 1 44.5 None 1
## 2 33.0 None 2
## 3 19.1 None 3
## 4 9.4 None 4
## 5 71.3 None 5
## 6 51.2 None 6
## 7 7.3 Tablet 1
## 8 21.0 Tablet 2
## 9 5.0 Tablet 3
## 10 4.6 Tablet 4xtabs(fecfat ~ subject + pilltype, data = fat)## pilltype
## subject None Tablet Capsule Coated
## 1 44.5 7.3 3.4 12.4
## 2 33.0 21.0 23.1 25.4
## 3 19.1 5.0 11.8 22.0
## 4 9.4 4.6 4.6 5.8
## 5 71.3 23.3 25.6 68.2
## 6 51.2 38.0 36.0 52.6Pour représenter les données de manière graphique, on peut utiliser un diagramme en ligne simple, à partir de la commande xyplot.
xyplot(fecfat ~ reorder(pilltype, fecfat), data = fat, groups = subject, type = "a",
xlab = "Pill type", ylab = "Fecal fat (g/day)", scales = list(y = list(at = seq(0,
80, by = 20))))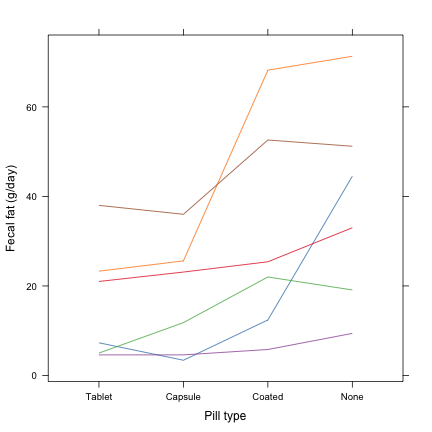
On notera que pour faciliter la lecture graphique, les niveaux du facteur d'intérêt ont été ordonné selon la valeur moyenne de la réponse mesurée.
Si l'on ne tient pas compte du facteur subjet, une ANOVA à un seul facteur (pilltype) ne permet pas de conclure à l'existence d'un effet du mode d'administration sur l'excès de graisse tel qu'il est mesuré :
summary(aov(fecfat ~ pilltype, data = fat))## Df Sum Sq Mean Sq F value Pr(>F)
## pilltype 3 2009 670 1.86 0.17
## Residuals 20 7193 360Clairement, la variance expliquée prise en compte par le facteur pilltype apparaît relativement faible (2009/(2009+7193) = 22 %), ce qui s'explique par le fait que la résiduelle contient actuellement la variance entre sujets que l'on pourrait vouloir éliminer (ou prendre en considération).
La première approche consiste à modéliser la variabilité inter-individuelle comme un facteur à part entière. Dans ce cas, le facteur est supposé à effet fixe.
summary(aov(fecfat ~ pilltype + subject, data = fat))## Df Sum Sq Mean Sq F value Pr(>F)
## pilltype 3 2009 670 6.26 0.00574 **
## subject 5 5588 1118 10.45 0.00018 ***
## Residuals 15 1605 107
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1À présent, la part de variance associée au facteur pilltype (\(\eta^2\) partiel) s'élève 2009/(2009+1605) = 56 % et le test F portant sur le rapport entre le carré moyen de l'effet et celui de la résiduelle est significatif. L'effet du facteur subject l'est également, ce qui n'est pas surpenant au vu de la variabilité des moyennes individuelles :
with(fat, tapply(fecfat, subject, mean))## 1 2 3 4 5 6
## 16.90 25.62 14.48 6.10 47.10 44.45On peut séparer ces deux sommes de carrés (subject et résiduelle) en considérant un terme d'erreur spécifique pour subject dans le modèle d'ANOVA.
summary(aov(fecfat ~ pilltype + Error(subject), data = fat))##
## Error: subject
## Df Sum Sq Mean Sq F value Pr(>F)
## Residuals 5 5588 1118
##
## Error: Within
## Df Sum Sq Mean Sq F value Pr(>F)
## pilltype 3 2009 670 6.26 0.0057 **
## Residuals 15 1605 107
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1On retrouve évidemment le même résultat pour le test F associé à l'effet de pilltype (les sommes de carrés associées au facteur et à la résiduelle ne changent pas), et la variance liée au facteur subjet est séparée (stratification) du reste des effets appelés "intra-sujets". Dans ce dernier modèle, seul le facteur pilltype est considéré comme facteur à effet fixe. La même approche sera utilisé dans le cas des plans à plusieurs facteurs intra-sujet, à ceci près que la formulation du terme d'erreur sera un peu plus compliquée. Voir Notes on the use of R for psychology experiments and questionnaires (§7.9) pour plus d'informations.
Dans les modèles d'ANOVA à mesures répétées, on fait l'hypothèse de sphéricité ou symétrie composée, qui suppose l'homogénéité des variances (comme dans l'ANOVA sur groupe indépendants) et des covariances (induite par la répétition des mesures chez un même sujet). Cette matrice de variance-covariance (VC) peut être affichée directement depuis le tableau de données, après l'avoir réagencé dans le format approprié (sujets en lignes et variables en colonnes, "wide").
library(reshape2)
fat.w <- acast(fat, subject ~ pilltype, value.var = "fecfat")
fat.w## None Tablet Capsule Coated
## 1 44.5 7.3 3.4 12.4
## 2 33.0 21.0 23.1 25.4
## 3 19.1 5.0 11.8 22.0
## 4 9.4 4.6 4.6 5.8
## 5 71.3 23.3 25.6 68.2
## 6 51.2 38.0 36.0 52.6cov(fat.w)## None Tablet Capsule Coated
## None 505.1 197.1 174.2 464.4
## Tablet 197.1 177.4 165.4 253.3
## Capsule 174.2 165.4 167.4 261.6
## Coated 464.4 253.3 261.6 588.7La diagonale de la matrice VC correspond aux variances des traitements,
apply(fat.w, 2, var)## None Tablet Capsule Coated
## 505.1 177.4 167.4 588.7tandis que les éléments hors-diagonaux correspondent aux estimations des covariances pour les séries de mesures (6 observations) prises deux à deux.
On peut vérifier qu'une régression multi-variable nous permet bien de retrouver les moyennes de groupes comme ceci :
lm(fat.w ~ 1)##
## Call:
## lm(formula = fat.w ~ 1)
##
## Coefficients:
## None Tablet Capsule Coated
## (Intercept) 38.1 16.5 17.4 31.1
## On définira également la "structure" des effets intra-sujet (pilltype) ainsi :
wsubj <- factor(levels(fat$pilltype))Enfin, on peut obtenir le tableau d'ANOVA correspondant à une ANOVA à un facteur intra-sujet à partir de la commande Anova du package car (Fox & Weisberg, 2011), cette commande renvoyant les résultats d'un modèle multivarié ou MANOVA (O’Brien & Kaiser, 1985) et de l'approche univariée qui nous intéresse dans le cas présent.
library(car)
summary(Anova(lm(fat.w ~ 1), idata = data.frame(wsubj), idesign = ~wsubj, type = "III"),
multivariate = FALSE)##
## Univariate Type III Repeated-Measures ANOVA Assuming Sphericity
##
## SS num Df Error SS den Df F Pr(>F)
## (Intercept) 15944 1 5588 5 14.27 0.0129 *
## wsubj 2009 3 1605 15 6.26 0.0057 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## Mauchly Tests for Sphericity
##
## Test statistic p-value
## wsubj 0.0619 0.0745
##
##
## Greenhouse-Geisser and Huynh-Feldt Corrections
## for Departure from Sphericity
##
## GG eps Pr(>F[GG])
## wsubj 0.556 0.025 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## HF eps Pr(>F[HF])
## wsubj 0.801 0.011 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Par souci de concision, on a supprimé l'affichage des tests multivariés. On retrouve le même tableau d'ANOVA avec un test F significatif au seuil conventionnel de 5 %. La commande Anova fournit un test de Mauchly pour l'hypothèse de sphéricité (voir help(mauchly.test)). Enfin, parmi les résultats figurent également les corrections des degrés de liberté de la statitique F (Greenhouse-Geisser et Huynd-Feldt) proposées pour le cas où l'hypothèse de sphéricité n'est pas vérifiée. On retiendra que l'approche par MANOVA, qui ne nécessite pas cette hypothèse de sphéricité, souffre également d'un manque de puissance dans le cas des petits effectifs, surtout lorsqu'ils sont déséquilibrés. Pour plus d'informations sur la sphéricité ou la symétrie composée, voir An introduction to sphericity.
Une approche alternative aux modèles précédents consiste à utiliser des modèles de régression linéaire incluant des effets aléatoires, en l'occurence des ordonnées à l'origine (intercept) spécifiques pour chaque sujet (approche conditionnelle). Les observations d'un même sujet sont modélisées en tant que données corrélées via l'effet aléatoire sujet-spécifique, et le modèle à intercept aléatoire permet de contraindre la matrice VC comme désiré.
library(nlme)
lme.fit <- lme(fecfat ~ pilltype, data = fat, random = ~1 | subject)
anova(lme.fit)## numDF denDF F-value p-value
## (Intercept) 1 15 14.266 0.0018
## pilltype 3 15 6.257 0.0057intervals(lme.fit)## Approximate 95% confidence intervals
##
## Fixed effects:
## lower est. upper
## (Intercept) 21.58 38.083 54.586
## pilltypeTablet -34.28 -21.550 -8.821
## pilltypeCapsule -33.40 -20.667 -7.937
## pilltypeCoated -19.75 -7.017 5.713
## attr(,"label")
## [1] "Fixed effects:"
##
## Random Effects:
## Level: subject
## lower est. upper
## sd((Intercept)) 8.001 15.9 31.58
##
## Within-group standard error:
## lower est. upper
## 7.232 10.344 14.794Le tableau d'ANOVA fournit le même résultat que dans l'approche avec aov (en ignorant le terme d'ordonnée à l'orgine). Les coefficients de régression s'interprétent de la même manière que dans le cadre d'une régression avec variable qualitative (utilisation de contrastes de traitement). On a également accès aux estimés des variances intra- et inter-sujets, cette dernière correspondant à la variance des effets aléatoires (les ordonnées à l'origine spécifiques de chaque sujet). La corrélation intra-classe, qui représente la proportion de la variance attribuable aux sujets (\(\sigma_s^2/(\sigma_s^2+\sigma_{\varepsilon}^2)\)), est estimée à 15.92/(15.92+10.342) = 0.703.
On peut retrouver la valeur du coefficient de corrélation intra-classe directement à partir des composantes de variance dérivées du tableau d'ANOVA à deux facteurs. Attention, les composantes de variance ne correspondent pas exactement aux carrés moyens estimés à partir de l'ANOVA.
aov2 <- aov(fecfat ~ pilltype + subject, data = fat)
ms <- anova(aov2)[[3]]
vs <- (ms[2] - ms[3])/nlevels(fat$pilltype) # subject
vr <- ms[3] # residuals
vs/(vs + vr)## [1] 0.7025Les valeurs prédites par le modèle s'obtiennent avec la commande predict, comme dans le cas de la régression simple (même si, en pratique et en théorie, la prédiction de données individuelles dans ce type de modèle est largement plus complexe que dans le cas où les coefficients de régression sont de simples paramètres).
fat$pred <- predict(lme.fit)On peut ensuite représenter graphiquement les prédictions individuelles du modèle et les comparer aux réponses observées affichées plus haut.
xyplot(pred ~ reorder(pilltype, fecfat), data = fat, groups = subject, type = "a",
xlab = "Pill type", ylab = "Predicted fecal fat (g/day)", scales = list(y = list(at = seq(0,
80, by = 20))))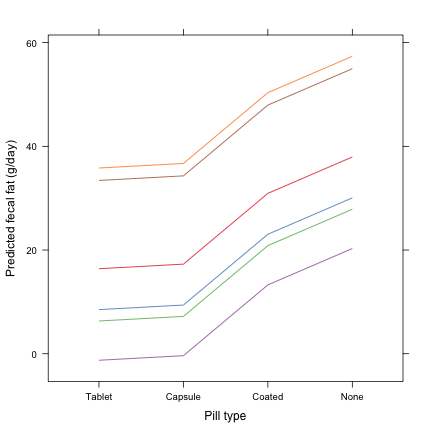
Dans le graphique résumant les valeurs prédites pour chaque individu, on voit clairement que les profils de variation entre les traitements sont comparables (par construction du modèle) et que seules les ordonnées à l'origine (ou, de manière équivalente, le niveau moyen) varient pour chaque individu.
Remarque.
Il est également possible d'imposer la contrainte de symétrie composée de l'ANOVA à mesures répétées à partir de la commande gls.
gls.fit <- gls(fecfat ~ pilltype, data = fat, corr = corCompSymm(form = ~1 | subject))
anova(gls.fit)## Denom. DF: 20
## numDF F-value p-value
## (Intercept) 1 14.266 0.0012
## pilltype 3 6.257 0.0036On pourrait également pondérer l'analyse en prenant en considération la variance des traitements.
update(gls.fit, corr = corSymm(form = ~1 | subject), weights = varIdent(form = ~1 |
pilltype))## Generalized least squares fit by REML
## Model: fecfat ~ pilltype
## Data: fat
## Log-restricted-likelihood: -74.18
##
## Coefficients:
## (Intercept) pilltypeTablet pilltypeCapsule pilltypeCoated
## 38.083 -21.550 -20.667 -7.017
##
## Correlation Structure: General
## Formula: ~1 | subject
## Parameter estimate(s):
## Correlation:
## 1 2 3
## 2 0.658
## 3 0.599 0.960
## 4 0.852 0.784 0.833
## Variance function:
## Structure: Different standard deviations per stratum
## Formula: ~1 | pilltype
## Parameter estimates:
## None Tablet Capsule Coated
## 1.0000 0.5927 0.5757 1.0796
## Degrees of freedom: 24 total; 20 residual
## Residual standard error: 22.47Fox, J., & Weisberg, S. (2011). An R companion to Applied Regression. Sage.
Howell, D. C. (1998). Méthodes Statistiques en Science Humaines. De Boeck.
O’Brien, R. G., & Kaiser, M. K. (1985). MANOVA method for analyzing repeated measures designs: An extensive primer. Psychological Bulletin, 97, 316–333.
Siegel, S. (1975). Evidence from rats that morphine tolerance is a learned response. Journal of Comparative and Physiological Psychology, 80, 498–506.
Vittinghoff, E., Glidden, D. V., Shiboski, S. C., & McCulloch. (2005). Regression Methods in Biostatistics. Linear, Logistic, Survival, and Repeated Measures Models. Springer.