
Résumé
Cette fiche de synthèse vise à présenter quelques cas d’application de la psychométrie dans le domaine des sciences de l’éducation. L’objectif est moins d’approfondir les techniques d’estimation utilisées que de fournir un aperçu de la richesse et de la diversité des approches de validation psychométrique. La présentation des tests SAT et du programme NAEP repose en grande partie sur les chapitres 33 et 32 du Handbook of Statistics, vol. 26 (Psychometrics), rédigés par M. von Davier, S. Sinharay, A. Oranje et A. Beaton, et J. Liu, D.J. Harris et A. Schmidt, respectivement.
Historiquement, les évaluations à grande échelle dans les « collèges » américains ont débuté dès 1926, avec le Scholastic Aptitude Test (SAT). Ce test était composé à l’origine de 9 sous-tests (définitions, problèmes arithmétiques, classification, langage, antonymes, séries de nombres, analogies, inférence logique et lecture de courts textes) et a été remplacé désormais par le SAT Reasoning TestTM, censé évaluer essentiellement les aptitudes verbales et de raisonnement mathématique et administré par le College Board. Vers la fin des années 50, un nouveau test, le ACT®; (ACT Inc., www.act.org) a rejoint le panel de tests proposés aux USA. L’idée était d’évaluer à la fois l’aptitude d’un élève à intégrer le collège américain, et les bénéfices qu’il pourrait tirer des enseignements dispensés en ces lieux. On retiendra que la différence fondamentale entre le SAT et le ACT est que le premier s’intéresse essentiellement aux capacités élaborées de raisonnement tandis que le second se focalise beaucoup plus sur la performance. Toutefois la corrélation entre les deux tests, du point de vue des scores délivrés aux candidats, est relativement bonne (0.92, n = 103525, [6]).
L’enjeu primordial est de préserver l’équité des évaluations car les tests sont administrés plusieurs fois par an. Pour cela, il est nécessaire d’assurer la qualité des tests (validité et la fidélité), ainsi que la standardisation des scores au travers des différentes sessions de test. Une bonne couverture de l’échelle de mesure, et une précision extrême aux points de césure font partie en effet des exigences associées aux tests à fort impact (high-stakes).
Concernant la conception des items, l’organisation générale est assez classique et se retrouve chez de nombreux concepteurs de tests (Figure 1). Nous nous intéresserons plus particulièrement à l’analyse des items et aux études de fidélité de mesure.
L’analyse d’items consiste à décrire le fonctionnement des items dans un test ou pour un certain groupe d’individus donné. Les principales caractéristiques d’un item concernent : sa difficulté relative, sa capacité à discriminer les individus selon leur niveau d’habileté, le comportement des distracteurs (dans le cas d’un item à choix multiple de réponse), le comportement de l’item entre différents groupes de répondants, le taux de non-réponses.
Difficulté relative de l’item. La mesure la plus simple de la difficulté d’un item pour un échantillon d’individus donné est l’indice de difficulté relative, encore appelé p-value. Il s’agit simplement de la proportion de candidats qui ont tenté de répondre à un item et y ont répondu correctement. Dans le cas du programme SAT, les p-values sont converties sur une échelle standardisée appelée delta index, de la manière suivante : δ = 13 + 4 × z, où (1 - p) est préalablement converti en un score z. Avec cette transformation, les δ et les p sont inversement reliés : plus p est petit, plus δ est grand, et plus l’item est considéré comme difficile.
Il est nécessaire de corriger ces valeurs pour tenir compte de la dépendance de ces estimations à l’échantillon de candidats. Pour cela, certains items présents dans des versions antérieures de test sont également intégrés au test, ce qui permet de standardiser les indices de difficulté grâce à une simple procédure de régression linéaire des nouvelles estimations sur les anciens paramètres de difficulté.
Enfin, notons que les items trop faciles ou trop difficiles apportent peu d’infomation sur les candidats.
Pouvoir discriminant d’un item. Tout item doit permettre de distinguer entre les candidats de haut niveau et ceux de plus faible niveau, par rapport au concept hypothétique objectivé dans le test. Un item sera considéré comme discriminant si un nombre proportionnellement plus grand de candidats de niveau élevé répond correctement à l’item en comparaison des candidats de plus faible niveau. On remarquera que la difficulté d’un item contraint d’une certaine manière son pouvoir discriminant, puisqu’un item très facile ne laisse que peu de variation résiduelle possible entre les différents individus.
L’indicateur statistique utilisé pour évaluer le pouvoir discriminant d’un item est le coefficient de corrélation bisériale (rbis), qui mesure la force de la liaison entre la performance à un item et celle observée en considérant l’ensemble des items. Un rbis faible ou négatif indique que l’item ne mesure sans doute pas la même chose que les autres items, tandis qu’une corrélation item-test très forte (i.e. proche de +1) suggère que l’item est probablement redondant par rapport à l’information apportée par les autres items qui composent le test.
L’inspection des corrélations item-test permet souvent de détecter des dysfonctionnements notables, comme par exemple une erreur de clé (label associé à la réponse correcte), une ambiguïté dans la formulation de la question, l’existence de plus d’une réponse correcte, etc.
De plus, à partir du score total, ACT sépare l’effectif en 3 groupes de candidats : faible, intermédiaire et élevé, à partir des 27eet 73epercentiles. Ces valeurs ont été choisies de sorte à maximiser la différence entre les scores moyens des groupes supérieur et inférieur, sous l’hypothèse que les erreurs de mesure sont identiques entre les deux groupes et que les scores de la population se distribuent selon une gaussienne [10].
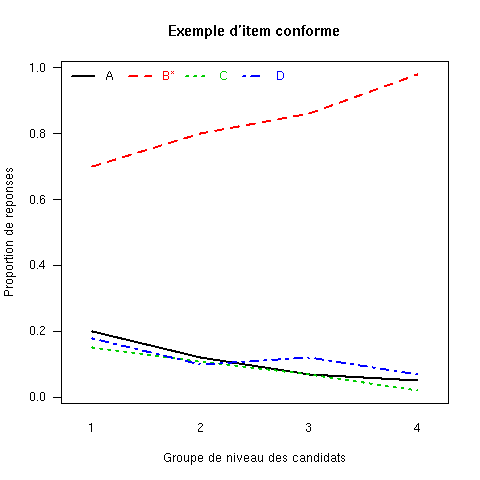
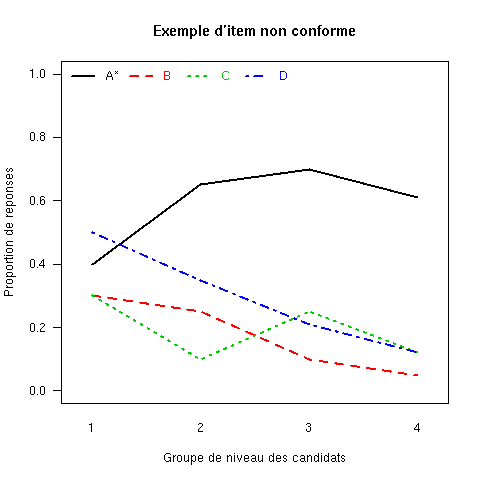
Analyse des distracteurs. La qualité d’un item ne s’évalue pas simplement au travers du fonctionnement de la clé, mais également à partir de la distribution des réponses aux distracteurs. Deux méthodes sont alors employées : ACT examine les proportions de réponse dans chacun des deux groupes extrêmes, tandis que SAT inspecte la courbe de réponse empirique à l’item (Figure 2).
 |  |
| (a) | (b) |
L’idée de l’analyse graphique des taux de choix des différentes modalités de réponse d’un item est de vérifier si :
Dans la figure 2, on vérifiera que le cas (a) vérifie bien ces propriétés alors que l’item illustré en (b) ne se conforme aux deux premières propriétés.
On l’aura compris : on recherche en général à ce que les candidats de niveau élevé choisissent le plus souvent la clé de l’item, tandis que les candidats de niveau faible se répartissent le plus uniformément possible sur les distracteurs ; les distracteurs non-choisis ne fonctionnent pas correctement et ceux pour lesquels on observe des taux de choix anormalement élevés sont le signe d’une erreur ou d’une ambiguïté de clé.
Fonctionnement différentiel d’un item. Le fonctionnement différentiel d’un item (DIF dans la littérature anglo-saxonne) est caractéristique du fonctionnement de l’item par rapport à différents sous-groupes d’individus parmi l’échantillon testé. Le DIF indique
« une différence au niveau des performances à l’item entre deux groupes d’individus comparables entre eux, c’est-à-dire lorsque les groupes sont appariés par rapport au concept hypothétique mesuré par le test. »
Dorans et Holland, 1993, [11], Trad. de l’auteur
Théoriquement, si les candidats de deux groupes différents (e.g. caractéristiques socio-démographiques, curricula, etc.) possèdent le même niveau d’habielté, leur probabilité de répondre correctement à l’item devrait être la même. Les deux groupes considérés sont appelés groupe focal et groupe de référence, le groupe focal étant le groupe sur lequel se concentre l’analyse. Il existe plusieurs manières de caractériser et quantifier le DIF, parmi lesquelles l’approche Mantel-Haenszel [12] et l’approche Standardization [13] utilisées par ACT et SAT.
La procédure Mantel-Haenszel (MH) est dérivée de la technique de Mantel-Haenszel pour les tableaux 2 × 2 × m, où m désigne les niveaux d’appariement entre les groupes. Dans le cas présent, il s’agit du score total au test, et on se retrouve avec un tableau de la forme
| Groupe | Score à l’item
| ||
| Correct | Incorrect | Total | |
| Focal | Rfm | Wfm | Nfm |
| Référence | Rrm | Wrm | Nrm |
| Total | Rtm | Wtm | Ntm |
L’hypothèse nulle correspondant au test MH est que « l’odds de répondre correctement à l’item à un niveau donné de la variable de conditionnement est le même dans le groupe focal et dans le groupe de référence ». Selon cette approche, l’odds-ratio commun, noté αMH, se définit comme
![[ ] [ ]
∑ RrmWfm--- ∑ RfmWrm---
αMH = Ntm ∕ Ntm ,
m m](NAEP0x.png) | (1) |
où m décrit les différents groupes de niveau. Cette valeur est convertie en une différence exprimée sur l’échelle standardisée des δ, i.e.
 | (2) |
Des valeurs positives de MH D-DIF sont en faveur du groupe focal, tandis que our des valeurs négatives c’est le contraire.
La procédure Standardization repose sur un principe simiaire, à ceci près qu’elle permet d’éviter la contamination causée par un mauvais ajustement du modèle de mesure. Plus précisément, ACT et SAT utilisent une différence de p-values standardisées, STD P-DIF [14]. Celle-ci est définie comme suit :
![[ ] [ ]
STD P-DIF = ∑ Wm-(P∑fm----Prm)- = ∑ ∑WmDm---
m m Wm m m Wm](NAEP2x.png) | (3) |
où Pfm = 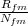 et Prm =
et Prm = 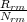 désignent les proportions de choix correct dans le
groupe focal et le groupe de référence, respectivement, à chaque niveau m du
score total. Dm désigne la différence entre ces deux quantités. L’originalité est
d’utiliser un facteur de pondération commun (Wm∕∑
mWm) à la fois
pour Pfm et Prm. En pratique, Wm = Nfm de sorte que le poids le
plus important est attribué aux différences entre Pfm et Prm pour les
niveaux du score total les plus fréquemment observés dans le groupe
focal.
désignent les proportions de choix correct dans le
groupe focal et le groupe de référence, respectivement, à chaque niveau m du
score total. Dm désigne la différence entre ces deux quantités. L’originalité est
d’utiliser un facteur de pondération commun (Wm∕∑
mWm) à la fois
pour Pfm et Prm. En pratique, Wm = Nfm de sorte que le poids le
plus important est attribué aux différences entre Pfm et Prm pour les
niveaux du score total les plus fréquemment observés dans le groupe
focal.
À ETS, ce type d’analyse se base sur le groupe des candidats de race blanche (groupe de référence) vs. les candidats afro-américains, hispanophones, asiatiques et les américains naturalisés (groupes focaux) ; de même, les femmes (groupe focal) sont comparées aux hommes (groupe de référence). À partir de la statistique MH D-DIF, ETS a proposé une classification du DIF en 3 niveaux : négligeable (A), intermédiaire (B) et important (C). Les items présentant un biais de fonctionnement de la catégorie C sont systématiquement écartés après la phase de prétest (pour être révisé avant d’être re-prétesté).
Longueur du test et taux d’omission L’analye des items inclut également la proportion d’individus ne terminant pas le test. Un taux d’omission important pour certains items peut être une indication que le test est trop long et que « l’échec » à l’item peut être expliqué par un manque de temps plutôt que par un manque de connaissance. Comme premier indicateur, on peut considérer la proportion de réponses aux 5 derniers items du test.
La longueur du test est également considérée sous l’angle de l’équité. Les tests SAT reposent sur une mesure différentielle de rapidité pour vérifier qu’un test ne favorise pas une certaine catégorie de la population. Ici, la notion de DIF renvoit à
existence of differential response rates between focal group members and matched reference group members to items appearing at the end of a section. (Dorans and Holland, 1993, p. 56)
Cette différence standardisée d’omission s’exprime comme
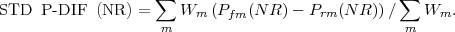 | (4) |
Les mêmes critères STD P-DIF sont utilisés pour construire une classification en 3 classes. Sur la période 2002–2003 par exemple, les items du SAT-V (verbal) ne présentent pas de biais homme/femme, alors que pour le SAT-M (maths) deux items ont été classés comme présentant un biais intermédiaire.
Les tests ACT et SAT sont des tests « à fort impact » (high-stakes) et sont administrés à plusieurs reprises, sous des formes différentes, durant la période scolaire. Afin que les scores soient comparables entre chaque administration du test, ce sont des scores standardisés (scaling) qui sont donnés aux candidats, et non les scores bruts. L’opération de normalisation (equating) vise à exprimer l’ensemble de ces scores sur une échelle de meure commune1 .
Scaling. Les scores standardisés sont définis de manière à conserver une interprétation cohérente au travers des différentes versions de test. Un score de 25 points au test ACT doit signifier la même chose, en termes de capacités, quelle que soit la version de test administrée au candidat. En revanche, les scores bruts peuvent varier d’une version à l’autre, tout en traduisant un même niveau de compétence : un score de 40 points sur une version peut être comparable à un score de 30 points sur une autre version de test si celle-ci est plus « difficile ». Les standards établis dans le domaine de l’éducation (Standards for Educational and Psychological Testing, [16]) précisent que les modalités de calcul des scores et la définition de l’échelle de mesure doivent être clairement explicitées afin de faciliter l’interprétation des scores (par les candidats et toute personne susceptible de prendre des décisions en conséquence).
Jusqu’à 1995, les scores SAT étaient basés sur une échelle allant de 200 à 800 points (moyenne, 500±100), construite à partir d’un échantillon de 10000 individus en 19412 . Le réétalonnage de l’échelle effectué par [17] suit les 7 propriétés suivantes :
L’application de ces critères par [17] a permis de construire une nouvelle échelle de moyenne 500 et d’écart-type 110, soit une gamme de scores observables de 170 à 830 points environ. De la sorte, les distributions marginales des scores aux épreuves verbales et mathématiques étaient identiques.
En ce qui concerne les scores ACT, leur étendue est de 1–36 points, avec une moyenne fixée à 18 points, sur la base de données recueillies sur un échantillon national en 1988. Les échelles de mesure ont été établies de sorte que l’erreur de mesure vaut environ 2 points pour chaque score composite, alors que les erreurs de mesure conditionnelles sont approximativement égales. L’étalonnage des scores ACT est effectué en 3 étapes. Dans un premier temps, les distributions des scores bruts pondérés ont été estimées sur un échantillon national et un groupe d’élèves de référence. Ensuite, ces distribution ont été lissées à partir d’un modèle de mélange de lois binomiale et beta [18, 19]. Les scores brutes ajustés ont finalement été utilisés pour créer des scores calibrés, après arrondis à l’entier le plus proche, tout en prenant en compte les contraintes de moyenne ± écart-type, d’absence de sauts dans la progression des scores sur l’échelle et de minimisation des scores à transformer. Les scores composites ACT ne constituent donc pas une échelle de mesure, à proprement parler, mais sont calculés comme la moyenne de 4 sous-scores.
L’arrivée d’une nouvelle tâche de production écrite dans les tests ACT a conduit au développement de deux nouvelles échelles. Le sous-score « Direct Writing » repose sur une grille de codage et s’étend de 2 à 12 points. L’échelle combinée « English/Writing » a été créée en standardisant les scores « English » et « Writing » avec des pondérations respectives de 2/3 et 1/3 et une transformation linéaire pour exprimer ces scores sur une échelle de 1–36 points. Encore une fois, les scores sont arrondis sous forme entière.
Equating. Une fois que les échelles ont été étalonnées, il reste à standardiser les scores de manière à ce qu’ils demeurent comparables, en termes d’interprétation, d’une version de test à l’autre (propriété d’interchangabilité). Deux types de standardisation sont utilisés pour les scores SAT : la méthode des groupes non-équivalents avec ancrage (NEAT, Nonequivalent groups anchor test design, Figure ??) et la méthodes des groupes équivalents ou aléatoires (EG, random/equivalent groups design). Lors de l’administration d’une nouvelle version de test, celle-ci est standardisée par rapport à plusieurs versions plus anciennes à l’aide de la méthode NEAT. Lorsque deux nouvelles versions de test sont administrées en parallèle, les scores de la première version sont standardisés à l’aide de la méthode NEAT tandis que ceux de la seconde version sont standardisés par la méthode EG. Les techniques de transformation de scores sont diverses et variées et peuvent être de type linéaire ou non-linéaire ; elles peuvent reposer sur les scores bruts directement, ou sur des modèles de scores vrais, et la standardisation peut être effectuée en utilisant une post-stratification.
La procédure de standardisation ACT repose sur un échantillon de candidats sélectionnés lors d’une session nationale qui sont soumis à un ensemble de version de tests. L’une des versions administrées est une version ancre incluant des items déjà calibrés et permet de la relier à l’échelle de mesure. Les autres versions de test sont de nouvelles versions. L’utilisation de groupes randomisés est une caractéristique importante de la procédure de standardisation dans la mesure où elle contribue à fournir une certaine « continuité » au niveau des échelles. La méthode utilisée pour la standardisation des scores sur ceux de la version ancrée est la méthode des rangs équipercentiles. Un score sur la version X et un score sur la version Y sont considérés équivalents s’ils sont au même renag percentile pour un groupe d’individus donné. Les résultats de la standardisation sont ensuite lissés à l’aide d’une méthode analytique décrite dans [20] et on conserve des valeurs entières dans les tables de conversion utilisées pour convertir les scores bruts en scores calibrés.
Des études de stabilité et un suivi régulier ont montré que les dessins de calibration des tests SAT et ACT fonctionnent de manière satisfaisante [21, 22]. Une façon d’évaluer une procédure de standardisation consiste à vérifier que la fonction de calibrage est invariante à travers différentes sous-populations, définies par exemple par le sexe ou le groupe ethnique des candidats, comme dans la population générale. En d’autres termes, est-ce que cette fonction de calibrage est la même dans la population générale et dans les différents sous-groupes [23] ? De telles études ont été réalisées pour le SAT-V et le SAT-M, en travaillant sur des sous-groupes définis par le sexe.
La possibilité de commettre des erreurs existe dans toutes les procédures de mesure des aptitudes cognitives, et il est par conséquent important de fournir à l’utilisateur un moyen d’évaluer la confiance que l’on peut avoir dans un score. Le terme d’« erreur » est souvent interprété comme synonyme d’inconsistence : dans quelle mesure un candidat obtiendrait un score identique s’il était soumis à un test de manière répétée ? Des scores soumis à des fluctuations aléatoires rendraient en effet les décisions reposant sur ceux-ci complètement irrationnelles.
Plusieurs facteurs peuvent influencer la consistance des scores ; ceci inclut : les facteurs liés au test lui-même (e.g. spécifications du test, nombre d’items, échelle de mesure), les facteurs liés au candidat (e.g. tendance à deviner les réponses, niveau de connaissance) et les facteurs situationnels (e.g. le niveau de fatigue d’un candidat, le type d’items administrés). Les indices de fidélité sont utilisés pour indiquer le degré de consistance espéré des scores d’un test en particulier. Comme il n’est généralement pas possible d’administrer de manière répétée les tests aux mêmes candidats, plusieurs indices ont été élaborés pour tenter d’estimer la fidélité de la mesure.
L’un des coefficients de fidélité les plus utilisés est un indicateur de la consistance interne du test. Ce que l’on appelle la fidélité test–retest est une estimation de la consistance des scores observés sur un individu à qui l’on administre le même test plus d’une fois. Comme il est difficile d’obtenir ce type de données en raison de possibles problèmes d’apprentissage ou de biais liés à l’administration répétée des mêmes items, on estime cette consistance interne à l’aide d’un indicateur spécifique calculé sur les données observées lors d’une seule session de test. Les tests ACT et SAT reposent sur l’indice KR-20 ; toutefois, comme le SAT utilise un système de notation particulier, l’indice original a été modifié en conséquence [24] :
![[ ∑ ∑ ∑ ]
--n-- --ni=1piqi +--ni=1k2p′iq′i +-2-ni=1kpip′i
fidélité = n- 1 1 - σ2t ,](NAEP6x.png) | (5) |
où pi est la proportion d’individus répondant correctement à l’item i, pi′ la proportion d’individus répondant de manière incorrecte, qi = 1 - pi, qi′ = 1 - pi′, k un facteur de correction pour le calcul des scores (0.250 pour les items à 5 modalités de réponse, 0.333 pour ceux à 4 modalités et 0 pour les réponses construites), n le nombre total d’items dans la sous-échelle du test, et σt2 la variance des scores totaux pour le type d’item considéré ou la partie de test. Cet indice est similaire au coefficient alpha (Cronbach).
Les estimations de la consistance interne sont faites sur les scores bruts. En revanche, les scores à partir desquelles les décisions sont effectuées sont les scores calibrés, donc il est important d’évaluer également la fidélité des scores calibrés. La fidélité de versions alternées est généralement estimée à partir de données répétées ou sur une session de test spéciale. Dans les deux cas, cela présente des désavantages : les candidats passant plusieurs sessions consécutives le font par choix personnel et ce sont généralement des candidats qui n’ont pas obtenus des scores aussi élevés que ce qu’ils auraient escompté lors de la première session.
Le programme National Assessment of Educational Progress (NAEP), piloté et administré par le National Assessment Governing Board et le National Center for Education Statistics (NCES), est un programme américain d’évaluation nationale du niveau de connaissances des élèves de grade 4, 8 et 12. Les tests sont organisés tous les deux ans auprès d’échantillons représentatifs de la population des élèves américains. L’évaluation couvre différents domaines comme la lecture, l’expression écrite ou les mathématiques. Des études longitudinales sont également réalisées auprès d’un public d’élèves âgés de 9, 13 et 17 ans. Une description complète de ce programme d’évaluation est disponible en ligne sur le site de NCES.
En raison de contraintes évidentes de temps, les élèves ne sont évalués que sur une partie des items assurant la couverture du domaine. De la sorte, on se retrouve dans une situation où seuls certains blocs d’items sont administrés à des groupes d’élèves, grâce à un plan incomplet équilibré (BIB dans la littérature anglo-saxonne). On a toujours deux blocs d’items appariés dans chaque manuel de test, et chaque bloc apparaît un même nombre de fois à chaque position (2 ou 3) dans ce dernier. La conséquence directe de cette organisation des items est que les scores des candidats ne sont pas comparables entre eux et il faut recourir à un modèle de réponse à l’item (MRI) permettant d’analyser les patterns de réponse, plutôt que les scores bruts, et de prendre en considération l’incertitude associée à l’évaluation (erreur de mesure). Chaque item peut être « relié » aux autres items à l’aide de contraintes d’égalité, grâce aux propriétés des BIB.
Plutôt que de considérer le score individuel, NCES s’intéresse à des groupes d’individus, de sorte que l’on dispose de suffisamment d’information pour avoir des estimations fiables du niveau de réussite. Le niveau d’habileté étant considéré comme un trait latent, la méthode mise en œuvre est un modèle de régression sur variables latentes incluant une variable prédictrice pour le groupe de candidats.
Pour chaque individu i, on considère un vecteur d’habileté à p dimensions, noté θi = (θi1,θi2,…,θip)′. Les différentes composantes de ce vecteur représentent les différents sous-tests d’un même domaine ; en mathématique, par exemple, cela peut être l’algèbre, la géométrie, etc. Le vecteur de réponse yi = (yi1,yi2,…,yip) de l’individu i apporte de l’information sur θik, et la fonction de vraisemblance (pour un individu quelconque) est de la forme :
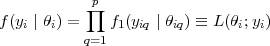 | (6) |
Les termes f1(yiq∣θiq) suivent un MRI univarié, généralement à 3 paramètres ou de type modèle de crédit partiel généralisé (GPCM). Chaque item d’une batterie de tests NAEP est conçu de manière à n’évaluer qu’un seul concept, de sorte que la multidimensionnalité évoquée ci-dessus demeure entre les items. La dépendance de f(yi∣θi) envers les paramètres des items peut être supprimée, pour faciliter les notations.
Si l’on ajoute à ce modèle décrivant l’habileté des individus un vecteur
xi = (xi1,xi2,…,xim) décrivant m caractéristiques socio-démographiques et
éducatives pour le candidat i, il est possible d’associer les deux types
d’information afin de mieux modéliser les performances des candidats.
Conditionnellement à xi, l’habileté d’un candidat θi suit une distribution
multivariée normale, i.e. θi∣xi ~iid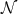 (Γ′xi,Σ). En général, NAEP collecte une
centaine de variables zi sur chaque candidat, et réalise une analyse en
composantes principales sur celles-ci ; seules les composantes xi qui expliquent
90 % de la variance totale au niveau des zi sont retenues pour les analyses
subséquentes.
(Γ′xi,Σ). En général, NAEP collecte une
centaine de variables zi sur chaque candidat, et réalise une analyse en
composantes principales sur celles-ci ; seules les composantes xi qui expliquent
90 % de la variance totale au niveau des zi sont retenues pour les analyses
subséquentes.
Sous ce modèle, L(Γ,Σ∣Y,X), la fonction de vraisemblance (marginale) de (Γ,Σ) basée sur les observations (X,Y ), est donnée par
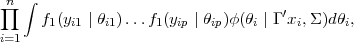 | (7) |
où n désigne le nombre d’individus et ϕ(⋅∣⋅,⋅) désigne la fonction de densité d’une loi normale multivariée.
Le modèle NAEP complet, combinant un modèle de réponse à l’item et un modèle de régression latente à deux niveaux, revient à un MRI multi-niveaux ou hiérarchique, dont on trouvera un exemple d’illustration avec R et Stata à la section 4. Outre la complexité de ce modèle, l’aspect le plus intéressant réside dans la possibilité d’estimer une erreur de mesure propre à l’instrument. En effet, la précision des paramètres de régression contribuent à l’erreur qui se reflète au niveau de la distribution latente, puisque l’information sur les groupes est fixée. À partir de là, il est possible de construire un modèle d’imputation pour avoir une estimation de l’habileté de tous les candidats en dérivant des valeurs probables (plausibles values, PV). La variance de ces PV peut alors être considérée comme une estimation de l’erreur de mesure.
L’estimation du modèle NAEP est réalisée à l’aide de programmes développés par ETS (MGROUP) et sur lesquels nous ne nous étendrons pas. Globalement, elle se déroule en trois étapes :
Il a été montré que Γ et Σ, pour des θi inconnus, peuvent être estimés grâce à l’algorithme EM [4, 5]. L’étape E, qui consiste à estimer à l’étape t + 1 les moyennes E(θi∣X,Y,Γt,Σt) et les variances Var(θi∣X,Y,Γt,Σt) a posteriori, peut être réalisée par intégration numérique, à l’aide de techniques bayésiennes ou par une approximation de Laplace. Les résultats par sous-groupe sont fournis sous la forme de PV, qui reviennent en fait à effectuer des imputations multiples en tirant les observations dans la distribution conditionnelle a posteriori des habiletés. L’algorithme est assez relativement simple :
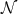 (
(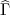 ,V (
,V (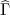 )), où V (
)), où V (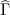 ) est la variance estimée de
l’estimateur du maximum de vraisemblance
) est la variance estimée de
l’estimateur du maximum de vraisemblance 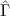 obtenu par l’algorithme
EM.
obtenu par l’algorithme
EM.
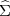 (estimée durant la procédure EM), on calcule la
moyenne i et la variance Σi pour l’estimé a posteriori de chaque
individu i dans l’échantillon.
(estimée durant la procédure EM), on calcule la
moyenne i et la variance Σi pour l’estimé a posteriori de chaque
individu i dans l’échantillon.
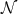 (i,Σi), indépendemment pour chaque
individu i = 1,2,…,N.
(i,Σi), indépendemment pour chaque
individu i = 1,2,…,N.Ces étapes sont répétées M fois, donnant lieu à M ensembles d’imputations (PV) pour chaque individu dans l’échantillon. Les PV sont utilisées comme indicateur de la valeur attendue a posteriori, avec d’autres statistiques tels les rangs percentiles ou les proportions de réussite par rapport à un seuil de référence.
Ensuite, puisque l’objectif de NAEP est de fournir des estimations du niveau d’habileté pour des sous-groupes spécifiques de candidats, il est nécessaire de calculer la valeur moyenne d’une certaine fonction de l’habileté dans le groupe considéré. Notons cette fonction g(θ). On pourra ainsi s’intéresser à estimer (1) g(θ) = θj (moyenne sur une sous-échelle), (2) g(θ) = ∑ jωjθj (moyenne d’un composite, avec pondération des items), ou (3) g(θ) = I∑ jω jθj>K (proportion d’individus avec un niveau moyen sur un composite qui est situé au-dessus d’un certain seuil).
Des alternatives ont été proposées à l’égard de cette technique d’estimation ; voir par exemple [2]. Celles-ci visent en particulier à pallier la nature complexe de la « structure » d’analyse et les approximations qui sont faites à chaque processus d’estimation.
Il existe plusieurs façons de modéliser un MRI hiérarchique, et plusieurs logiciels disposent des procédures appropriées. Nous nous concentrerons sur R et Stata.
[3]
En fait, il existe même un package R, mlirt, qui permet de construire ce genre de modèle [1]. L’exemple fourni par l’auteur porte justement sur les données recueillies lors des études PISA 2003.
Les premières étapes visent à construire la matrice de réponse que l’on va utiliser dans le modèle hiérarchique. Pour ne pas biaiser les résultats, on ne retient que les individus ayant fourni une réponse à au moins 10 items.
La dernière instruction vise à construire la matrice des variables liées aux écoles (n = 150).
Le premier modèle testé est un modèle nul. On l’évaluera de la manière suivante :
La fonction mlirtout fournit les valeurs estimées pour les candidats.
Le modèle complet peut être évalué à l’aide des instructions suivantes :
Contrairement à R, Stata dispose d’une interface graphique. Il existe néanmoins un macro-language qui permet de faire tourner des scripts conçus à l’aide d’un simple éditeur de texte, et, comme R, on a accès à un ensemble d’extensions disponibles sur le web. Parmi celles-ci, mentionnons gllamm conçu par S. Rabe-Hesketh et coll. [7, 9, 8] et disponible à l’adresse www.gllamm.org/.
[1] Fox, J.-P. (2007). Multilevel IRT Modeling in Practice with the Package mlirt. Journal of Statistical Software, 20(5), 1–16. www.jstatsoft.org/v20/i05
[2] M. von Davier and S. Sinharay (2007). An Importance Sampling EM Algorithm for Latent Regression Models. Journal of Educational and Behavioral Statistics, 32(3), 233–251.
[3] Lockwood, J.R., Doran, H. and McCaffrey, D.F. (2003). Using R for Estimating Longitudinal Student Achievement Models. R News, 3(3), 17–23. cran.r-project.org/doc/Rnews/Rnews_2003-3.pdf
[4] Mislevy, R. (1984). Estimating latent distributions. Psychometrika, 49(3), 359–381.
[5] Mislevy, R. (1985). Estimation of latent group effects. Journal of the American Statistical Association, 80(392), 993–997.
[6] Dorans, N.J. (1999). Correspondences between ACTTM and SAT I®; scores. College Board Report No. 99-1, ETS Report No. 99-2, College Entrance Examination Board, New York, NY.
[7] Rabe-Hesketh, S., Skrondal, A. and Pickles, A. (2004). Generalized multilevel structural equation modelling. Psychometrika, 69(2), 167–190.
[8] Rabe-Hesketh, S. and Skrondal, A. (2008). Multilevel and Longitudinal Modeling using Stata (2nd Edition). College Station, TX : Stata Press.
[9] Zheng, X. and Rabe-Hesketh, S. (2007). Estimating parameters of dichotomous and ordinal item response models using gllamm. The Stata Journal, 7(3), 313–333.
[10] Millman, J. and Greene, J. (1989). The specification and development of tests of achievement and ability. In : Linn, R.L. (Ed.), Educational Measurement, 3rd ed. American Council on Education and Macmillan, New York, pp. 335–366.
[11] Dorans, N.J. and Holland, P.W. (1993). DIF detection and description : Mantel-Haenszel and Standardization. In : Holland, P.W., Wainer, H. (Eds.), Differential Item Functioning. Lawrence Erlbaum Associates, Hillsdale, NJ, pp. 35–66.
[12] Holland, P.W. and Thayer, D.T. (1988). Differential item performance and the Mantel-Haenszel procedure. In : Wainer, H., Braun, H.I. (Eds.), Test Validity. Lawrence Erlbaum Associates, Hillsdale, NJ, pp. 129–145.
[13] Dorans, N.J. and Kulick, E. (1986). Demonstrating the utility of the standardization approach to assessing unexpected differential item performance on the Scolarship Aptitude Test. Journal of Educational Measurement, 23, 355–368.
[14] Dorans, N.J. and Kulick, E. (1983). Assessing unexpected differential item performance of female candidates on SAT and TSWE forms administered in December 1977 : An application of the standardization approach. ETS Report 83-9, Educational Testing Service, Princeton, NJ.
[15] Kolen, M.J. and Brennan, R.L. (2004). Test Equating, Scaling, and Linking. Methods and Practices. Springer-Verlag.
[16] American Educational Research Association, American Psychological Association, National Council on Measurement in Education (1999). Standards for Educational and Psychological Testing. AERA, Washington, DC.
[17] Dorans, N.J. (2002). The recentering of SAT scales and its effect on score distributions and score interpretations. College Board Report No. 2002-11, College Entrance Examination Board, New York, NY.
[18] Lord, F.M. (1965). A strong true score theory, with applications. Psychometrika, 30, 239–270.
[19] Kolen, M.J. (1991). Smoothing methods for estimating test score distributions. Journal of Educational Measurement, 28, 257–282.
[20] Kolen, M.J. (1984). Effectiveness of analytic smoothing in equipercentile equating. Journal of Educational Statistics, 9, 25–44.
[21] McHale, F.J. and Nimmeman, A.M. (1994). The stability of the score scale for the scholastic aptitude test from 1973 to 1984. ETS Statistical Report SR-94-24, Educational Testing Service, Princeton NJ.
[22] Hanson, B.A., Harris, D.J. and Kolen, M.J. (1997). A comparison of single- and multiple linking in equipercentile equating with random groups. Paper presented at the Annual Meeting of the American Educational Research Association, Chicago, IL.
[23] Dorans, N.J. and Holland, P.W. (2000). Population invariance and the equatability of tests : Basic theory and the linear case. Journal of Educational Measurement, 37(4), 281–306.
[24] Dressel, P.L. (1940). Some remarks on the Kuder-Richardson reliability coefficient. Psychometrika, 5, 305–310.