The Racket engine has finally been ported to Chez Scheme. Note that bytecode vs. machine code may impact memory use. #scheme

BlurHash is a compact representation of a placeholder for an image.

Must read: Tour of Python Itertools. #python

A Regular Expression Matcher.

Recursion is a win. This fundamental programming technique almost always leads to smaller, cleaner and more elegant code than the equivalent written with explicit loops, and that is the case here. The idea of peeling off one matching character from the front of the regular expression and from the text, then recursing for the rest, echoes the recursive structure of the traditional factorial or string length examples, but in a much more interesting and useful setting.

Enhanced music listening on macOS.

Fish-like autosuggestions for zsh.

I happily and enthusiastically paid for all that music. But now? Every time I see the $14.99 charge for our Apple Music family plan hit my checking account, I wince. I pay it begrudgingly because I feel like I have no other choice. — Begrudgingly

Same for me. I prefer to use native app (Safari, Apple Mail, etc.) FWIW. However, I should note that the revamped iTunes app looks just weird.

What’s under the hood is rarely what you expect. Our current tech stack is heavily optimized and a lot of optimizations are really just dirty tricks. — Math keeps changing

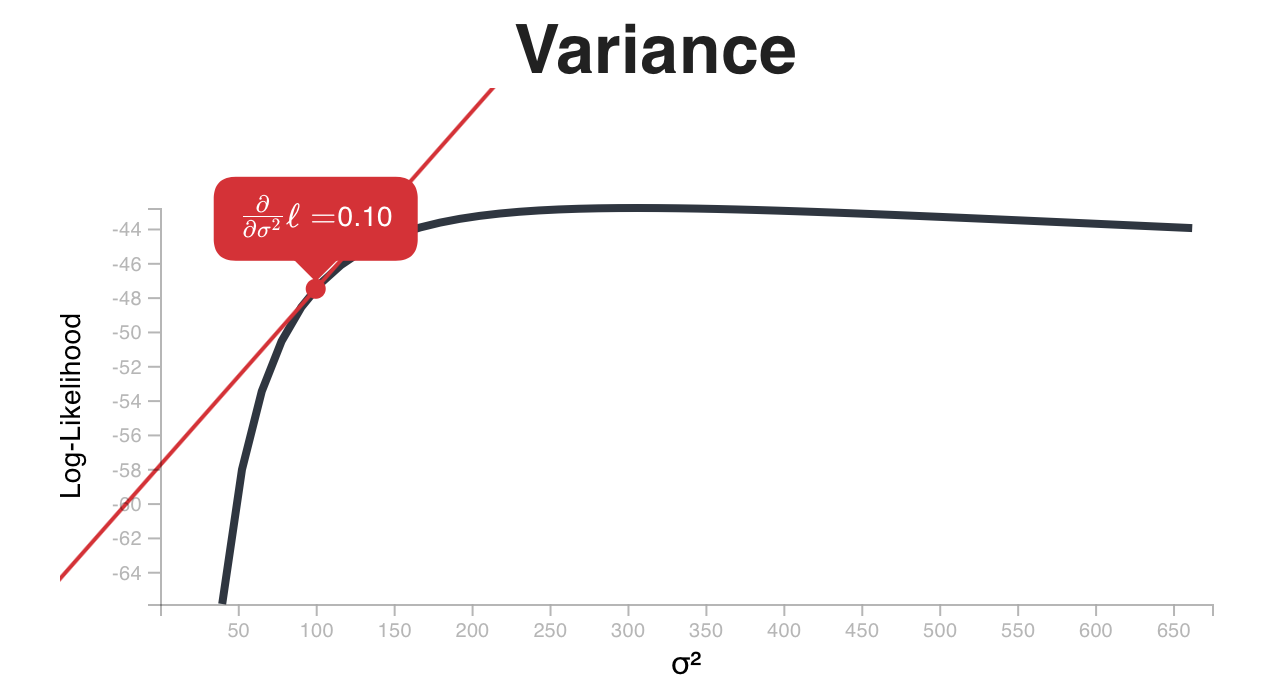
I’ve been perusing Kristoffer Magnusson artwork when I was teaching inferential statistics, and here is a nice post on understanding Maximum Likelihood.

Reliable computer systems must handle malfunctioningcomponents that give conflicting information to different parts of the system. This situation can be expressed abstractly in terms of a group of generals of the Byzantine army camped with their troops around an enemy city. Communicatingonly by messenger, the generals must agree upon a common battle plan. However, one or more of them may be traitors who will try to confuse the others. The problem is to find an algorithm to ensure that the loyal generals will reach agreement. It is shown that, using only oral messages, this problem is solvable if and only if more than two-thirds of the generals are loyal; so a single traitor can confound two loyal generals. With unforgeable written messages, the problem is solvable for any number of generals and possible traitors. Applications of the solutions to reliable computer systems are then discussed. — The Byzantine Generals Problem (PDF)