In his Mathematical Recreations and Essays, W.W. Rouse Ball mentions two ways to estimate the value of of $\pi$ to a few digit places “using probability.” I would say this is more of a frequentist estimation problem than a purely probabilistic method since it involves collecting experimental data.

The first approach considers a number of equidistant parallel straight lines lying on a plane, distance apart $a$; if we drop a stick of length $l < a$ on to the plane, then the probability that it will fall so as to lie across one of the lines is $2l / \pi a$. This means we can estimate this quantity, and therefore $\pi$, by repeating this experiment a large number of times. For instance, $\pi = 3.1419$ was found with 1120 trials by Captain Fox in 1864.¹

The second approach relies on prime numbers: If two numbers are written down at random, the probability that they will be prime to each other (i.e., co-prime) is $6/\pi^2$. Here is a little simulation in Mathematica that considers the first 250 positive integers to mimic the author’s report of an experiment in which each of 50 students wrote down 5 pairs of numbers at random, where it was found that 154 of the pairs were found to consist of co-prime numbers:

In[14]:= Total[Boole[Array[CoprimeQ, {250, 250}]], 2]/250^2 // N
Out[14]= 0.608752
In[17]:= Sqrt[6/%]
Out[17]= 3.12094

Assuming you have enough RAM, we would get closer with a larger sample size:

In[18]:= Total[Boole[Array[CoprimeQ, {10000, 10000}]], 2]/10000^2 // N
Out[18]= 0.60795
In[19]:= Sqrt[6/%]
Out[19]= 3.14153

Finally, here is a plot of random co-prime numbers in the range $[3;100]$, as suggested in the help desk:

In[15]:= randomCoprime[x_Integer] :=
  RandomChoice[Pick[Range[x], CoprimeQ[x, Range[x]]]];
ListPlot[{#, randomCoprime[#]} & /@ RandomInteger[{3, 100}, 500]]

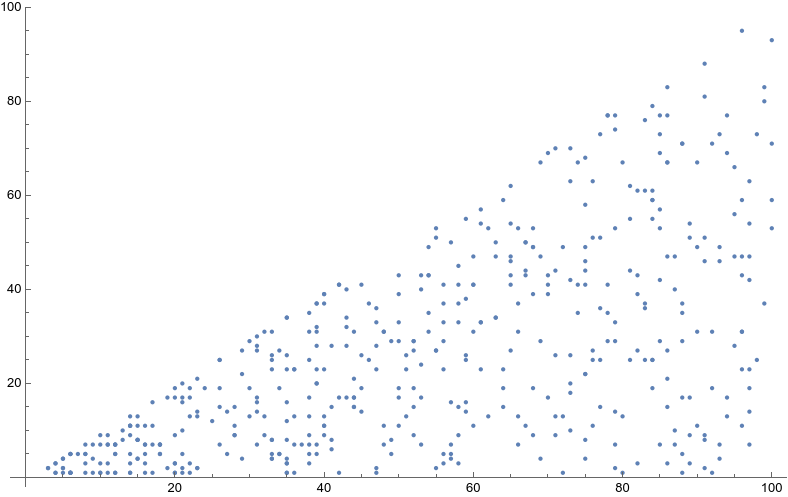
The above function could be used to draw random integer instead of the first consecutive integers used in the previous simulation.