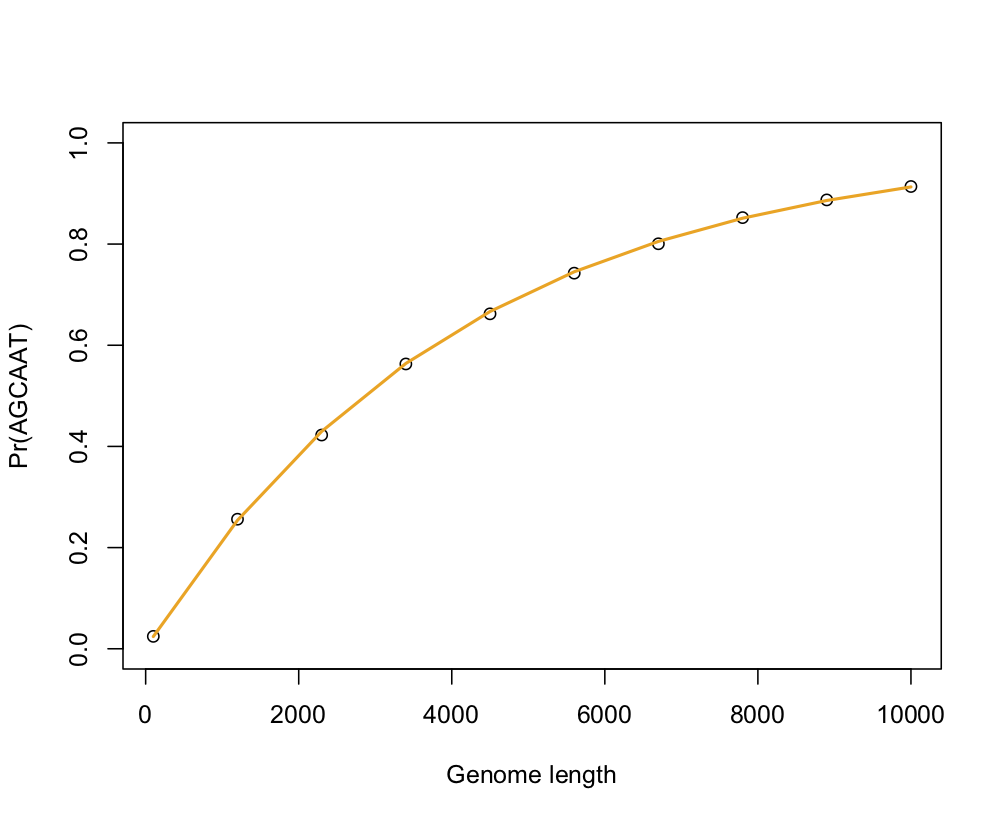
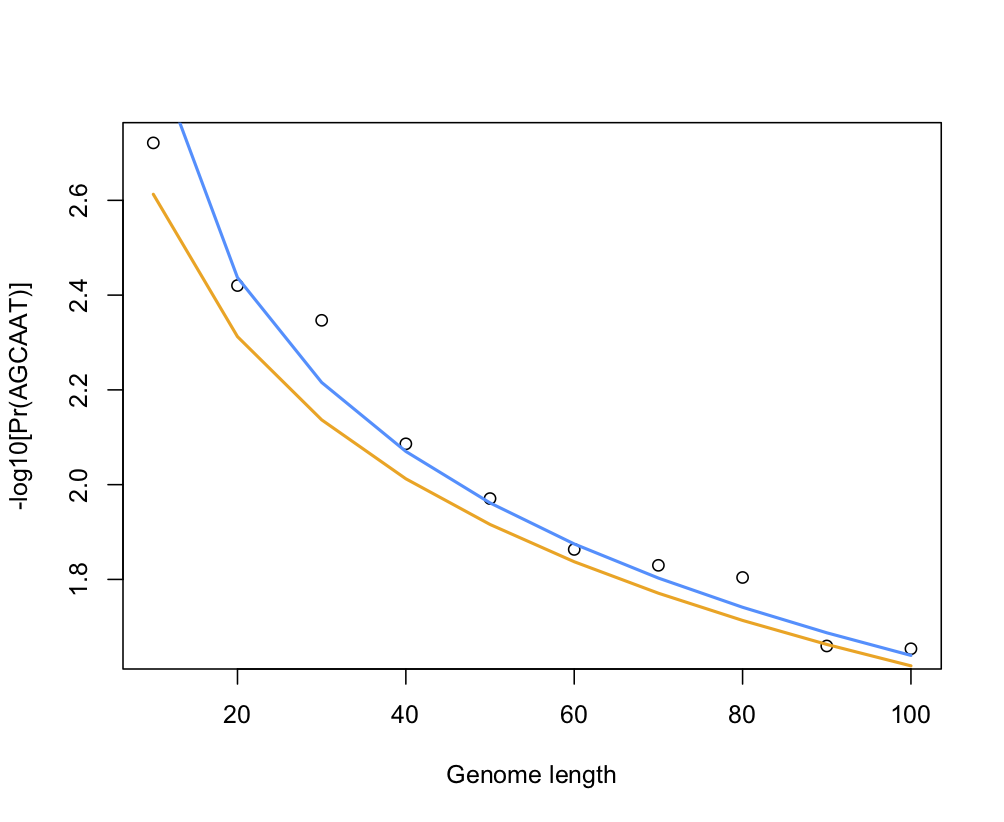
What is the probability of finding a given DNA sequence in a window of a given size? As a first approximation, we could consider that all nucleotides are independent one from the other, so that for a four-letter alphabet, each nucleotide appears with a probability 1/4. This is not true because GC content varies from one genome to the other, but let’s continue with this simple scheme. Now, consider a sequence of size k and a window of size n (n much smaller than the genome length). If all nucleotides are assumed independant, then the probability of not finding this particular sequence is $(1 - 1/4^k)$ (using the complementary is useful to avoid dealing with the number of times this sequence can appear) times the total number of positions available in the window (n or n - k + 1, but if $k \ll n$ this correction factor can be omitted). Hence the answer: $1 - (1 - 1/4^k)^n$.

The following pictures shows the results of a little simulation in R (points are empirical estimates while blue and orange lines are theoretical expectations with or without the correction factor for sequence length, 1 - k — which confirms that accounting for the sequence length only matters for small window size):

Now, we know that nucleotides are not independant at all. We would eventually need to compute the joint probability of all nucleotides in a sequence, e.g., $\Pr(AGCAAT) = \Pr(A)\Pr(G|A)\Pr(C|AG)\ldots$, which might work when k is small, but in the long run it becomes quite cumbersome to compute all conditional probabilities. Markov to the rescue: Let us consider that the probability of given nucleotide is only dependent on the preceding one, that is:

$$\Pr(x) = \Pr(x_1)\prod_{i=2}^k\Pr(x_i|x_{i-1}).$$

Then the idea is to specify transition probabilities like we did in an other post, to describe the probability of having, say, a G after a A, and so on. A working example using R code is provided on Cross Validated. Moreover, if such a Markov chain is allowed to have an end state, it can account for specific ending nucleotides, e.g. STOP codons. You end up with a distribution over all possible next states, and those parameters can be estimated using maximum likelihood. As an example, let’s consider our sample sequence {A, G, C, A, A, T}. We have the following ML estimates: $\Pr(A) = 3/6$, $\Pr(G) = \Pr(C) = \Pr(T) = 1/6$. Having larger sequences, or simply more sample sequences, would help refine those estimates, of course. But we could also rely on a Bayesian approach and Laplace estimation (the same technique is used in M-gram models or any stochastic process that assumes a sequence of random variable $X_i$ where $\{x_1, \dots, x_2\}$ is observed).

Higher-order Markov models are available, though. For instance we could allow the Markov model to have some “memory”, i.e. instead of considering $\Pr(x_i|x_{i-1})$, we can work with $\Pr(x_i|x_{i-1}, x_{i-2}, \dots, x_{i-k})$, with $k$ small enough in order to avoid the trap of a too large number of joint probabilities (we need $\mathcal{O}(4^{k+1})$ parameters for a $k$-th order Markov model). Bioinformatics: The Machine Learning Approach, by Baldi & Brunak, has some other interesting discussion on modeling biological sequences (e.g., section 3.1 and chapter 11). Finally, for a more detailed discussion of the above review, see Burr Settles' great lecture on Probabilistic Sequence Models (PDF, 59 pp.).