I often read questions on the use of Factor Analysis (FA) with categorical data, typically binary (yes/no) indicators or ordinal responses (e.g., Likert-type items). Here is a brief list of references that justify its use in this context, and provide comparison with other measurement models (mostly from the Item Response Theory literature).

Usually, my first thought when someone ask whether we can use exploratory or confirmatory FA on dichotomous or polytomous items is a paper by Jan de Leeuw: Takane and de Leeuw, On the relationship between item response theory and factor analysis of discretized variables, Psychometrika (1987) 52(3):393.

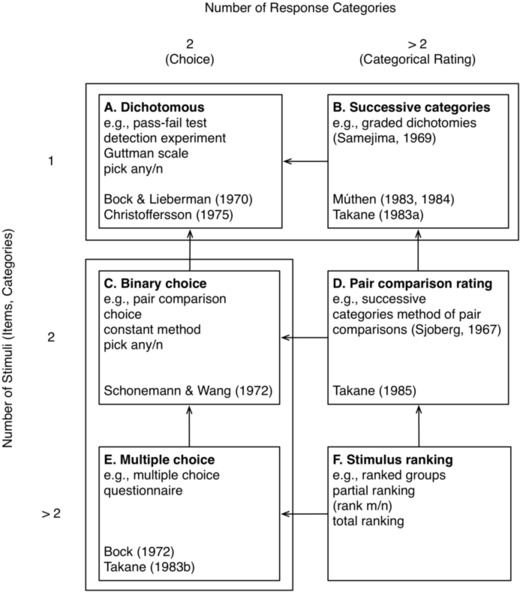
Basically, this paper demonstrates that Bock’s marginal likelihood method for a two-parameter IRT model with gaussian errors (’normal ogive model’) is equivalent to traditional factor analysis for categorical data, in case of dichotomous (Christoffersson, 1975) and ordered polytomous items (Muthén, 1984). Generalization to the case of unordered polytomous items is also discussed in Section 4. The “taxonomy of data for the IRT and FA models” (Table 1, p. 403) encompasses a wide range of models and applications:

Another paper that I often provide as a more recent reference is Kamata and Bauer, A Note on the Relation Between Factor Analytic and Item Response Theory Models, Structural Equation Modeling (2008) 15:136.

In this paper, the authors extend the work of Takane and de Leeuw by considering four different parameterizations for binary FA models and their relations to parameters estimated in a 2-PL model. A working example serves as an illustration of how item parameters are recovered with SAS PROC MIXED or the BILOG-MG program.

Of course, a lot more of papers on latent variable modeling with categorical indicators have been published by Bength Muthén in the last 20 years.

Beside the equivalence between item parameters in those models–discrimination (IRT) or loading (FA)–another concern in statistical modeling of individual responses to discrete items is that of the dimensionality of the scale. Although there exist variants of IRT models to cope multi-scale multi-items instruments, the above articles only deal with unidimensional scales. In a next post, I will discuss the comparison between IRT and FA approach to multidimensional scale, based on the following article: Reise, Morizot, and Hays, The role of the bifactor model in resolving dimensionality issues in health outcomes measures, Quality of Life Research (2007) 16:19.

Meanwhile, there are a couple of references from this article that provide additional insights into the propinquity between IRT and FA to scaling of individual differences:

1. Christoffersson, A (1975). Factor analysis of dichotomized variables. Psychometrika, 40, 5-32.
2. Knol, DL and Berger, MPF (1991). Empirical comparison between factor analytic and multidimensional item response models. Multivariate Behavioral Research, 26, 457-477.
3. Muraki, E and Carlson, JE (1995). Full-information factor analysis for polytomous item responses. Applied Psychological Measurement, 19, 73-90.
4. Bock, RD, Gibbons, R, and Muraki, E (1988). Full information item factor analysis. Applied Psychological Measurement, 19, 73-90.
5. Swygert, KA, McLeod, LD, and Thissen, D (2001). Factor analysis for items or testlets scored in more than two categories. In D Thissen & H Wainer (eds.), Test scoring (pp. 217-250). Mahwah, NJ: Erlbaum.
6. Flora, DB and Curran, PJ (2004). An empirical evaluation of alternative methods of estimation for confirmatory factor analysis with ordinal data. Psychological Methods, 9, 466-491.
7. Gibbons, RD, Bock, RD, Hedecker, D, Weiss, DJ, Segawa, E, Bhaumik, DK, Kupfer, DJ, Frank, E, Grochocinski, VJ, and Stover, A (2007). Full-information item bi-factor analysis of graded response data. Applied Psychological Measurement, 31, 4-19.
8. Jöreskog, KG and Moustaki, I (2006). Factor analysis of ordinal variables with full information maximum likelihood.
9. McDonald, RP (2000). A basis for multidimensional item response theory. Applied Psychological Measurement, 24, 99-114.
10. Muthén, B (1984). A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators. Psychometrika, 49, 115-132.

Of note, the so-called Full-Information Item Factor Analysis is available in the mirt R package, by Phil Chalmers. For other statistical package, see John Uebersax webpage on Binary Data Factor Analysis and Multidimensional Latent Trait/Item Response Theory (IRT) Models.

Finally, there is a great step-by-step illustration of factor analysis on dichotomous data using R on Cross Validated.