Mostly draft versions of never ending blog posts…

Customizing iPython

(April 2010)

Although I used it as my default Python shell, I never read the complete documentation (as usual). Now, I discovered that we can start iPython with different profile, with one being a complete numeric-oriented.

$ ipython -p numeric

Numeric and Gnuplot Python package are required. They can be installed from source, but in both case I had to manage the config files. For Gnuplot, if like me you happen to install the dev version of late 2009 (Version 4.2 patchlevel 6, Sep 2009) to benefit from the interactive x11 device (which was broken in the official release of Gnuplot 2.1), you will need to change the default terminal which is set to 'aqua' in gp_macosx.py. Then you can byte compile the file then install the package as usual:

$ python 
>>> import py_compile 
>>> py_compile.compile('gp_macosx.py') 
>>> ^D
$ sudo python setup.py install

Numeric is an old package for scientific computing. It has been superseded by Numpy since. However, it still includes useful features. To compile on a Mac, you will need to comment the redefinition of gettimeofday in ranf.c:

$ cd Packages/RNG/Src
$ grep gettimeofday *.c

Also, set your CFLAGS as '-arch x86_64' before launching the following:

$ python setup.py build

Dynamic visualization with GGobi

(April 2010)

I remember that two years ago, when I was reading Selvin’s book, Modern Applied Biostatistical Methods Using S-Plus, 1998, I tried to reproduce his Fig. 2.26 (p. 108) which illustrates spinning visualization. I used a very dirty R script (spin_plot.R) to generate 360/k figures (PNG) in a folder, then converted them to an animated frame (using ImageMagick, 20/100 sec. per frame, with infinite looping) using something like:

$ convert -delay 20 -loop 0 fig*.png spin_plot.gif
$ display spin_plot.gif

The result is shown below, with data generated as data <- replicate(3, rnorm(100)) in R.

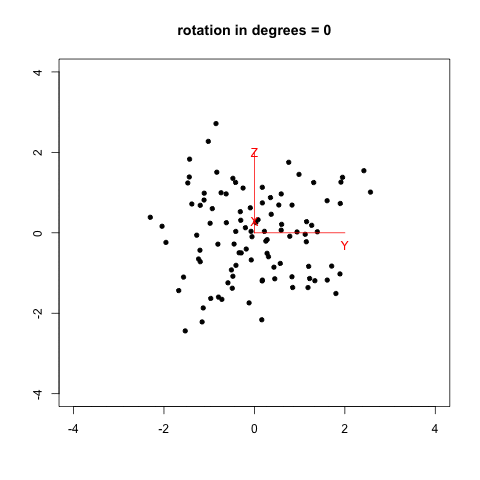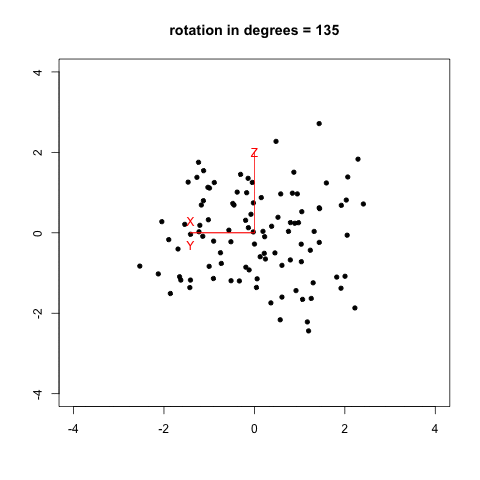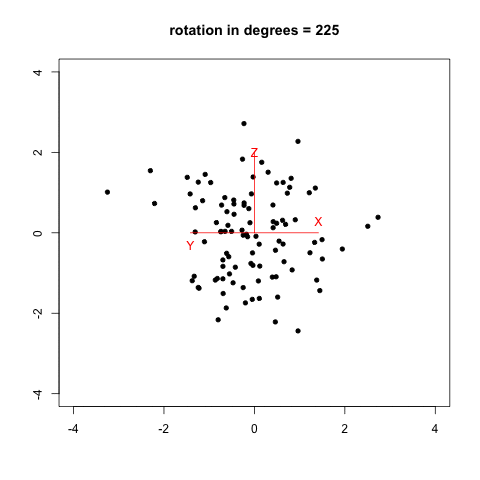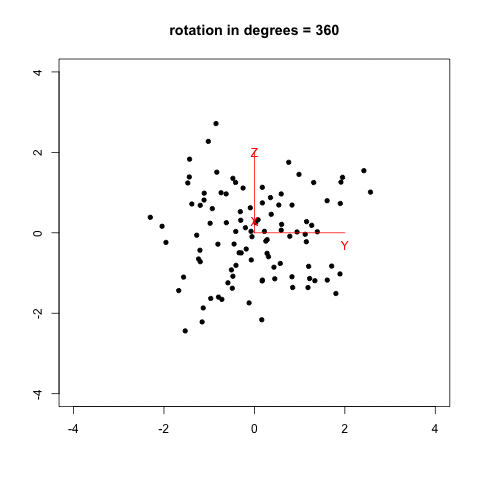
Now, we can do much better with GGobi and Projection Pursuit.

Cross-cultural issues in quality of life studies

(April 2010)

I am just reading a new book on Health-related quality of life (HRQL), Quality of Life Impairment in Schizophrenia, Mood and Anxiety Disorders, edited by M.S. Ristner and A.G. Awad (Springer, 2007). It is not so recent but it is one of the unusually good review on HRQL studies and their applications in clinical settings or clinical trials. An older one is Quality of Life and Pharmacoeconomics in Clinical Trials, from B. Spilker (Lippincott Wiliams & Wilkins, 1995), but it’s already 1,259 pages long!

The definition of quality of life as stated by the WHOQOL working group⁽¹⁾ is reproduced below:

Quality of life is an individuals’ perceptions of their position in life in the context of the culture and value systems in which they live, and in relation to their goals, expectations, standards and concerns. It is a broad ranging concept affected in a complex way by the persons’ physical health, psychological state, level of independence, social relationships and their relationship to salient features of their environment.

We may be tempted to add those questions raised by Elkinton⁽²⁾ some forty years ago

How does the physician protect the proper quality of life of the individual patient? How can the quality of life be improved…? Into which programs of preventive and therapeutic medicine should the resources of society be put to achieve the maximum in health and quality of life for all members of that society?

A historical account of HRQL research can be found in the review of Medina et al.⁽³⁾

From a psychological perspective, two questions (at least) are to be answered by the researcher: (1) what factors impact HRQL, and (2) what factors impact its subjective reporting.

Now, the NIH has prescribed that all research projects about health disparities or epidemiological studies in general must include minorities to the extent that it seems appropriate to the study under consideration. The same applies in clinical trials, unless researchers are seeking a very homogeneous group of patients.

In genetic epidemiology, for instance, it is common to consider “culture” a one of the main covariate. I quoted the term culture since we more often see words like ethnicity or ancestry in place of culture or even race. Following the IOM⁽⁴⁾ definition, race encompasses inter-individuals variations at both the biological and behavioral level, but see Hernandez and Blazer⁽⁵⁾ (Chapter 5) for an extended discussion on this topic.

Shields et al.⁽⁶⁾ recommend avoiding the term of race although race and ethnicity appear to bear some explanatory power when predicting disease risk (in mental or more common health problems):

(…) with the exception of the health disparities context, in which self-identified race remains a socially important metric, race should be avoided or used with caution and clarification, as its meaning encompasses both ancestry… and ethnicity (…)

Chapter 4 (M. Bullinger, S. Schidt, and D. Naber) is entirely devoted to the development of health-related instruments across cultures.

The authors also make a clear distinction between functional impairments as reported in most HRQL instrument and the subjective consequences of these functional limitations. Moreover, “in order to fully capture the concept (of quality of life), health status measurements should be operationalized both via clinical information and self-reports, which is in line with the classical approach to health indicator research” (p. 70).

Again, I have prepared a quick and dirty BibTeX file and its HTMLized version, holding the aforementioned references and moreover.

References

1. WHOQoL Group. Study protocol for the World Health Organization project to develop a quality of life assessment instrument (WHOQOL). Quality of Life Research, 1993, 2: 153-159.
2. Elkinton, JR. Medicine and the quality of life. Annals of Internal Medicine, 1966, 64(3): 711-714.
3. Medina, A, Moreno, MJ, Segura, C, Lillo, R, and Dening, TR. Quality of life and medicine: a historical note. History of Psychiatry, 1996, 7(26): 225-229.
4. IOM (Institute of Medicine). The Unequal Burden of Cancer: An Assessment of NIH Research and Programs for Ethnic Minorities and the Medically Underserved. Washington DC: National Academy Press, 1999.
5. Hernandez, LM and Blazer, DG (Eds). Genes, Behavior, and the Social Environment: Moving Beyond the Nature/Nurture Debate. National Academies Press, 2006.
6. Shields, A, Fortun, M, Hammonds, EM, King, PA, Lerman, C, Rapp, R, and Sullivan, PF. The use of race variables in genetic studies of complex traits and the goal of reducing health disparities: A transdisciplinary perspective. American Psychologist, 2005, 60(1): 77-103

Visual psychophysics with Python

(June 2010)

I rediscovered the VisionEgg library which is a powerful Python package for building visual and auditory psychophysical experiments, among others. More generally, this can be viewed as a wrapper for Pygame.

When I started my PhD, I was used to the Psychophysics toolbox for MATLAB (but I haven’t any Mac at that time) and it was pretty cool. I learned 3 or 4 years ago that most of my visual stimulations could be made thanks to Pygame but this is the end of the story: I never had to program any other experiment since then. Googling about the Psychtoolbox, I learned that it is now compatible with Octave (a great news since most of my old Matlab scripts never ran on Octave!), but see the aforementioned wiki.

Setup is quite straightforward, although compilation of gl_qt.c failed. Most of the demo scripts are running.

A note about PyQt

To get a working Qt binding for Python, you will need the PyQt4 which also depends on sip. Both packages can be downloaded from http://www.riverbankcomputing.com/. Note, however, that they must be compiled as 32 bits since no 64 bits Qt is actually available (it is planned for version 4.7).

$ python configure.py --arch i386
$ make
$ sudo make install
$ file /System/Library/Frameworks/Python.framework/Versions/2.6/bin/sip
/System/Library/Frameworks/Python.framework/Versions/2.6/bin/sip: Mach-O executable i386

For PyQt, just use

$ python configure.py --use-arch i386
$ make

It’s about 10’ of compilation where a warning is issued at each step, Support for this version of Mac OS X is still preliminary. You should end up with something like

g++ -headerpad_max_install_names -arch i386 -single_module \
  -dynamiclib -o libpythonplugin.dylib pluginloader.o \
  moc_pluginloader.o  -F/Library/Frameworks -L/Library/Frameworks \
  -framework Python -framework QtDesigner -framework QtScript \
  -framework QtXml -framework QtGui -framework Carbon \
  -framework AppKit -framework QtCore -lz -lm \
  -framework ApplicationServices 

As can be seen, several tools are built at once (QtGui, QtHelp, QtMultimedia, QtNetwork, QtOpenGL, QtScript, QtScriptTools, QtSql, QtSvg, QtTest, QtWebKit, QtXml, QtXmlPatterns, phonon, QtAssistant, QtDesigner), all as Framework. After make install, many files will be installed in Python system-wide directories, as well as the /Developer directory (e.g. libpythonplugin.dylib).

import sys
from PyQt4 import QtGui
app = QtGui.QApplication(sys.argv)
btn = QtGui.QPushButton("Installation seems ok!")
app.setMainWidget(btn)
btn.show()
app.exec_loop()

R/Qt, an overview

(July 2010)

Last year, I attended the DSC 2009 conference in Copenhagen (a very nice place!). Sarkar Deepayan had a talk about a newly designed graphical interface based on Qt. To illustrate the power of this glyph-based device, he showed how a scatterplot matrix of 100 random gaussian vectors renders very slowly through lattice compared to QT-based plot.

Although not ready for production, the qtpaint package offers some visualization functionalities that I’d like to experiment. Obviously, the installation doesn’t get right out of the box…

Here is a couple of tricks I used to compile a 64-bits version of qtpaint.

• Install Qt, not from binary package which is 32-bits only, but from source: wget http://get.qt.nokia.com/qt/source/qt-everywhere-opensource-src-4.6.2.tar.gz (153 Mb), then ./configure -arch x86_64; make (I think a flag like -cocoa might also works) and sudo make install: the compilation takes about 3 hours (on a 2.8 GHz Core 2 Duo), so be patient :)
• Download the SVN qtinterfaces bundle package from Rforge, e.g. svn checkout svn://svn.r-forge.r-project.org/svnroot/qtinterfaces
• CMake ≥ 2.8.1, grab the source from here, then ./bootstrap; make and sudo make install upon completion (use gcc and g++ to compile, not the llvm suite, e.g. export CXX=g++; export CC=gcc)
• Build the R package qtbase, using R CMD build qtbase in the svn directory (go to pkg/ from svn root directory)
• Install the R package with R CMD install qtbase_0.6-8.tar.gz; this is also rather long and you will see several passes over the package components (smoke, etc.)

Ok, it’s a bit long when one’s just want to give R/qt a try.

Weighted vs. simple summated scale scores

(August 2010)

I just ran across this abstract: Weighted index explained more variance in physical function than an additively scored functional comorbidity scale, from Resnik, L., Gozalo, P., and Hart, D.L., in press in Journal of Clinical Epidemiology

Objective: 1) examine association between the Functional Comorbidity Index (FCI) and discharge functional status (FS); 2) examine impact of FCI on FS when added to comprehensive models; and 3) compare additive FCI with weighted FCI and list of condition variables (list). Study Design and Setting: Patients were drawn from Focus On Therapeutic Outcomes, Inc. (FOTO) database (1/1/06–12/31/07). FS collected using computer adaptive tests. Linear regression examined association between FCI and FS. Three methods of including functional comorbidities (FC) were compared. Results: Relationship between FCI and FS varied by group (range, 0.02–0.9). Models with weighted index or list had similar R2. Weighted FCI or list increased R2 of crude models by <0.01 for cervical, shoulder, and lumbar; by 0.01 for wrist/hand, knee, and foot/ankle; by 0.02 for hip; by 0.03 for elbow; and by 0.08 for neurological. Addition of FCI to comprehensive models added <0.01 to R2 (all groups). Weighted FCI increased R2 by <0.01 for cervical, lumbar, and shoulder; by 0.01 for wrist/hand, hip, knee, and foot/ankle; by 0.02 for elbow; and by 0.04 for neurological; whereas list increased R2 by <0.01 for cervical, shoulder, and lumbar; by 0.01 for knee and foot/ankle; by 0.02 for elbow, wrist/hand, and hip; and by 0.05 for neurological. Conclusion: List of comorbidities or weighted FCI is preferable to using additive FCI.

Variations around the Lasso

(October 2010)

The Lasso page contains most of what is needed to get started with lasso regression and technical details about L1-penalty. In what follows, I will just review some of the well-known applications of the Lasso and several case-specific derivations.

Some results support the idea that forward selection performs as well as the Lasso⁽⁶⁾, and the same authors have proposed the Forward-Lasso Adaptive SHrinkage (FLASH), based on the LARS algorithm.

It can be shown that the LARS algorithm yields the entire path of Lasso solutions. Quoting the Lasso page, the LARS algorithm basically reads:

1. Start with all coefficients b_j equal to zero;
2. Find the predictor x_j most correlated with y;
3. Increase the coefficient b_j in the direction of the sign of its correlation with y. Take residuals r=y-ŷ along the way. Stop when some other predictor x_k has as much correlation with r as x_j has;
4. Increase (b_j, b_k) in their joint least squares direction, until some other predictor xm has as much correlation with the residual r;
5. Continue until: all predictors are in the model.

To get Lasso solutions, we just have to modify the above steps as follows: if a non-zero coefficient hits zero, remove it from the active set of predictors and recompute the joint direction.

• LARS is available in biglars
• glmnet R package, with implementation detailed in the Journal of Statistical Software

Group Lasso

The basic idea of Group Lasso^(1-3) is to achieve shrinkage on block of covariates, that is some blocks of regression coefficients are exactly zero. Blockwise Sparse Regression⁽⁴⁾ extends that idea to general loss functions and GLMs.

Fused Lasso

• Matlab SLEP package⁽¹⁵⁾
• cghFlasso, fused lasso for CGH data

Graphical Lasso

• R glasso
• Matlab code is available on Mark Schmidt’s webpage.

References

1. Meier, L, van de Geer, S, and Bühlmann, P. (2008). The group lasso for logistic regression, Journal of the Royal Statistical Society Series B, 70, Part 1, 53-71.
2. Roth, V and Fischer, B (2008). The Group-Lasso for Generalized Linear Models: Uniqueness of Solutions and Efficient Algorithms. Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland.
3. Friedman, J, Hastie, T, and Tibshirani, R (2010). A note on the group lasso and a sparse group lasso.
4. Kim, Y, Kim, J, and Kim, Y (2006). Blockwise sparse regression. Statistica Sinica, 16, 375-390
5. Bach, FR (2008). Consistency of the Group Lasso and Multiple Kernel Learning. Journal of Machine Learning Research, 9, 1179-1225.
6. Radchenko, P and James, GH (2009). Forward-LASSO with Adaptive Shrinkage.
7. Friedman, J, Hastie, T, and Tibshirani, R (2007). Sparse inverse covariance estimation with the graphical lasso. Biostatistics
8. Huang, J, Ma, S, and Zhang, C-H (2008). Adaptive lasso for sparse high-dimensional regression models. Statistica Sinica, 18, 1603-1618.
9. Tibshirani, R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society Series B, 58, 267–288.
10. Martinez, JG, Carroll, RJ, Müller, S, Sampson, JN, and Chatterjee, N (2009). Empirical Performance of Crossvalidation with the Adaptive Lasso in a Genomics Context. IAMCS.
11. Mutshinda, CM and Sillanpä, MJ (2010). Extended Bayesian LASSO for Multiple Quantitative Trait Loci Mapping and Unobserved Phenotype Prediction. Genetics,
12. Krämer, N, Schäfer, J, and Boulesteix, A-L, (2009). Regularized estimation of large-scale gene association networks using graphical Gaussian models. BMC Bioinformatics, 10, 384.
13. Rinaldo, A (2008). Properties and Refinements of The Fused Lasso.
14. Liu, J, Yuan, L, and Ye, J (2010). An Efficient Algorithm for a Class of Fused Lasso Problems. KDD'10, July 25–28, 2010, Washington, DC, USA.
15. Tibshirani, R, Saunders, M, Rosset, S, Zhu, J, and Knight, K Sparsity and smoothness via the fused lasso.
16. Liu, J, Ji, S, and Ye, J (2010). SLEP: Sparse Learning with Efficient Projections.

Medicine 2.0

(December 2010)

Back from the Medicine 2.0 conference held in Maastricht. I must admit this was not really what I expected to find (ePRO, CAT system, etc.), but it was nevertheless interesting to see what is actually headed under eHealth and how it applies in real study.

It appears that very few RCTs are carried out with truly distant intervention programs, but electronic coaching, especially in psychiatric or psychological follow-up, are increasingly in use, at least in the USA. What is striking is that numbers clearly show that there are more blacks or hispanics people that are actually using (or owning) a mobile device than white. I would have expected that socio-economic factors will moderate this difference nowadays, but this is apparently not the case.

Many ways to fit a Rasch model

(December 2010)

Here is a short memo on the many ways to fit a Rasch Model. After describing the two most commonly used Likelihood-based approaches (marginal and conditional), I shall move onto Bayesian models as implemented in the MCMCpack and DPpackage.

Classical approaches: marginal and conditional approaches

Basically, omitting the joint ML approach (as in Lord⁽¹⁾ or the Winsteps software), we will consider two different ways of estimating parameters of a Rasch Model, namely maximizing of the marginal likelihood (MML) or conditional likelihood (CML). Actually, I drafted a quick and dirty memo some time ago, but it’s in French and is roughly taken from Baker and Kim.⁽²⁾ The very brief idea are summarized in the following paragraphs.

Following the MML approach, as implemented in the ltm package, we assume that individual effects are random realizations taken from a population density, g(θ_p|ψ). This density is characterized by a vector of parameters, ψ, from an unknown population, and that has to be estimated like the parameters of the fixed effects β_i. The likelihood to be maximized looks like

$$ \ell_{\text{MML}}(\beta,\psi)=\prod_{p=1}^P\int_{-\infty}^{+\infty}\Pr(Y_{pi}=y_{pi}\mid\theta_p)g(\theta_p\mid\psi)d\theta_p. $$

Depending on the assumptions made on g(θ_p|ψ), three approaches are available, namely a non-parametric, semi-parametric, and parametric approach. In most parametric settings, we consider an N(0;σ²) (σ unknown). In this case, the likelihood can be written as

$$ \ell(\beta,\sigma_{\theta}^2)=\prod_{p=1}^P\ell_p(\beta,\sigma_{\theta}^2)=\prod_{p=1}^P\int\Pr(y_p\mid\beta,\theta_p)\phi(\theta_p\mid 0,\sigma_{\theta}^2)d\theta_p, $$

where $l_p$ denotes the contribution of person p to the marginal likelihood.

On the contrary, under the CML approach, subject-specific effects disappear from the likelihood (hence the name “conditional”) which now reads

$$ \ell_{\text{CML}}(\beta)=\prod_{p=1}^P\Pr(Y_{p1}=y_{p1},\dots,Y_{pI}=y_{pI}\mid s_p), $$

and is maximized with respect to β. The total score s_p is a sufficient statistic for the specific person effect θ_p. After conditioning, the probability of observing a given response pattern no longer depends on this effect, but only on the sufficient statistic. The eRm package offers many IRT models that are members of the Rasch family.

The disadvantage of this method is that it does not allow for any inference on the individuals, unless we consider item parameters as known values (after their estimation) and plug them into the joint likelihood.

In their JSS paper, Extended Rasch Modeling: The eRm Package for the Application of IRT Models in R, Patrick Mair and coll. clearly pointed to the advantages of using CML

Mixed-effects logistic model

Doug Bates already illustrated the use of his lme4 package to fit a Rasch Model. In fact, this is basically the way the marginal approach works. Again, the problem is merely from a conceptual point of view, namely that of treating person parameters as random effects as was discussed in the preceding section.

Using Poisson regression

An example was already provided in Carstensen 2nd book series on Log-linear models (chapter xx).

Estimation with MCMC

Estimation with Dirichlet

The semi-parametric Rasch model proposed by San Martin et al.⁽³⁾ is shortly described in the online help for DPMrasch(). Well, I must admit I had a hard time to read it as is, so that, for convenience, I put it here with proper LaTeX formatting. Even after having that, I needed to resort the San Martin’s article to understand the notation used therein.

$$ \eta_{ij}=\theta_i-\beta_j $$

with the following prior distributions

$$ \left\{\begin{array}{rcl} \theta_i\mid G & \sim & \int\mathcal{N}(\mu;\sigma)G(d\mu, d\sigma) \newline \beta\mid \beta_0, S\beta_0 & \sim & \mathcal{N}(\beta_0;S\beta_0) \newline G\mid\alpha, G_0 & \sim & \text{DP}(\alpha G_0) \end{array}\right. $$

Independent hyper-priors are also given as

$$ \left\{\begin{array}{rcl} \alpha\mid a_0,b_0 & \sim & \Gamma(a_0,b_0) \newline \mu_b\mid m_0, s_0 & \sim & \mathcal{N}(m_0;s_0) \newline \sigma_b^2\mid \tau_{b1}, \tau_{b2} & \sim & \Gamma(\tau_{b1|2},\tau_{b2|2}) \newline \tau_{k2}\mid \tau_{s1}, \tau_{s2} & \sim & \Gamma(\tau_{s1|2},\tau_{s2|2}) \end{array}\right. $$

More details can be found in the corresponding JSS article and R News. In the meantime, I worked through the online example which is based on simulated data with N=250 subjects and k=40 binary items.

References

1. Lord, F.M. (1980). Applications of item response theory to practical testing problems. Mahwah, NJ: Erlbaum.
2. Baker, F. B., & Kim, S.-H. (2004). Item response theory: Parameter estimation techniques (2nd ed.). New York: Marcel Dekker.
3. San Martin, E., Jara, A., Rolin, J.-M., and Mouchart, M. (2009). On the Analysis of Bayesian Semiparametric IRT-type Models. In preparation.

Fitting Rasch model with JAGS

(December 2010)

In a recent post, I talked about the idea of fitting IRT models within a Bayesian framework. Usually, this is done with the BUGS sofwtare. Here is an illustration of Rasch modelling with JAGS.

Let’s consider the data on verbal aggression described by De Boeck and Wilson in Explanatory Item Response Models (Springer, 2004). The data set is described pp. 7-10. It consists in

Of note, the data are now available in the lme4 package.

Classical IRT approaches

There are many ways of estimating parameters from a Rasch model based on this data, and we shall concentrate on the marginal and conditional likelihood appraoch. The ltm and eRm packages implement these two methods, respectively. Note that a mixed-effects model will yield comparable results in the former case.

The Bayesian way

Let’s now turn our attention to JAGS. I already post some notes on Bayesian analysis with R, and the following steps are not very different. Basically, we need to specify our model, that is our prior distributions and starting values. As there is already a BUGS example included in the on-line documentation, let’s look at it first:

model {
# Rasch model
   for (j in 1:N) {
      for (k in 1:T) {
         logit(p[j,k]) <- beta*theta[j] - alpha[k];
         r[j,k] ~ dbern(p[j,k]);
      }
      theta[j] ~ dnorm(0,1);
   }
# Priors
   for (k in 1:T) {
      alpha[k] ~ dnorm(0,0.0001);
      a[k] <- alpha[k] - mean(alpha[]);
   }
   beta ~ dnorm(0,0.0001) T(0,);

Clearly, the parametrization adopted here is (θ_j - β_k) for individual j responding to item k.

Apache Mahout and Hadoop

(December 2010)

Today, I start playing with Hadoop and Mahout which is a “scalable machine learning library that supports large data sets.” Distributed computing has gained a large interest from the scientific community in these recent years, especially because of the ever growing amount of data that one has to proceed, from neurorimaging or genetics data to the analysis of social networks or media products.

Distributed computing

Distributed computing is now widely used for solving complex tasks with huge data set, e.g. data mining, forecasting. I am particularly interested in its application in large-scale studies like the one commonly found in genome-wide association or gene screening applications. But this is definitively not the purpose of this post.

Some time ago, I read an interesting article about Xgrid on MacResearch. Specifically, the author presented a complete example of running a fasta job that will scan across all 23 chromosomes. According to Apple ACG , Xgrid

allows almost anyone to easily run a set of calculations on many machines using machine-dependent parameters. You can keep your focus on the science and mathematics and not distract yourself learning the details of setting up a network of computers. You don’t have to become a system administrator and set up user accounts and manage the network topology.

What is Hadoop?

The Hadoop framework comes with core utilities and a distributed file system management (HDFS) which allows to create “multiple replicas of data blocks and distributes them on compute nodes throughout a cluster to enable reliable, extremely rapid computations.” The core Hadoop essentially consists in a set of libraries and services for running jobs. Assuming you have a dedicated file system to store data I/O, Hadoop take care of launching and distributing jobs. A Single Node Setup is described on Hadoop website. I personally put it in /usr/local/share/hadoop-install/hadoop-0.21.0 and symlinked it to Hadoop for short. Then, I follow the instructions step by step.

The map/reduce paradigm was introduced by Google some years ago as a framework for distributed computing on large data sets. Using a large number of computers, or nodes, which altogether belong to a cluster, the idea is to break a problem into small pieces that are distributed to these nodes that in turn can also address sub-problems to their coworkers. Upon completion, solutions can be sent back to the master node. So, the basic idea is that of the divide and conquer principle. The MapReduce documentation has some good tutorials to get starting with.

There are several other projects that are actually hosted under the Apache foundation, e.g., Hive and Pig to name a few. As of September 2010, they become “top-level” Apache projects. I shall discuss them in another post.

About Mahout

Mahout has been released not so recently I guess, but I just discovered it! The goal of Mahout is to build scalable machine learning libraries. Scalable should be understood as a general purpose framework, with efficient algorithm and data structures for moderate to large data sets. Actually, it seems that the four main topics of Mahout are:

• Recommendation mining (infer from users’ choice the best set of item that they might like)
• Clustering (identify related documents)
• Classification (assign to an unlabelled document its correct category)
• Frequent itemset mining (uncover relationships between items based on their frequency of co-occurences)

Isabel Drost, one of the cofounder of Mahout, has some online material which I found quite useful to get a first feeling of what Mahout might be good at; see e.g., Apache Mahout Making data analysis easy . Of note, she’s also actively involved in the NoSQL paradigm.

The original work was described at NIPS'06 in the following paper: Map-Reduce for Machine Learning on Multicore . Actually, several algorithms are available, including the one I am interested in, namely Clustering (at the time of this writing, hierarchical clustering doesn’t seem to be available yet) and Random Forests. Interestingly, Mahout also features collaborative filtering.¹ I still have to figure out what the links with preference-based models in psychometrics, if any. In R, two packages are devoted to frequent itemsets: arules and recommenderlab.