This post is about multi-group partial least squares path modeling (PLS-PM). There is already a useful list of references on this blog post. As the author noticed, ensuring measurement invariance is often thought of as a prerequisite before dwelling into multi-group comparison, at least in the psychometric literature that I am familiar with. From a measurement perspective, this is easily understandable since we need to ensure that we are indeed measuring in a similar way the exact same construct in specific subpopulation.

I am not sure this apply to more general SEM or PLS models which may include a mix of reflexive and formative indicators, but anyway we will consider that PLS-PM is used to answer the same kind of questions as factor analysis does in general, and that we are interested in PLS approaches because of their relaxed assumptions regarding data properties (sample size, distribution, etc.). A nice overview of PLS approaches in SEM is available in Monecke et Leisch, semPLS: Structural Equation Modeling Using Partial Least Squares (JSS 2012, 48(3)).

In the aforementioned blog, I found two references that deal with multi-group comparison issues in the context of PLS-PM. Both are available as PDFs:

1. Chin, W. W., Mills, A. M., Steel, D. J., & Schwarz, A. (2012). Multi-group invariance testing: An illustrative comparison of PLS permutation and covariance-based SEM invariance analysis. 7th International Conference on Partial Least Squares and Related Methods, May 19-22, 2012, Houston.
2. Visinescu, L. (2012). PLS group comparison: A proposal for relaxing measurement invariance assumptions. 7th International Conference on Partial Least Squares and Related Methods, May 19-22, 2012, Houston.

The Handbook of Partial Least Squares, edited by Esposito Vinzi et coll., further includes several chapters dedicated to multi-group comparison using permutation-based approaches.

In the R packages semPLS and plspm the authors offer bootstrap and/or permutation-based procedures to assess the significance of path coefficients in single or multi-group settings. I should note that there is also a general purpose package for multi-group analysis on CRAN: multigroup. Since I am mostly using factor analysis or item response models, I generally rely on lavaan and semTools for multi-group comparisons.

Back to PLS models, Gaston Sanchez (author of plspm) provides some illustration of multi-group comparison in his handbook, PLS Path Modeling with R, using resampling methods (bootstrap t-test and permutation). The plspm::plspm.groups() function simplify the task since it allows the user to specify a PLS model (inner and outer blocks, modes) and a grouping factor. However, it is assumed that we are interested in inspecting and comparing each parameter estimates in different subsamples, which of course is what generally matters. But what if we are only interested in assessing the model as a whole, at the level of model parameters (and not other indices of model quality like RMSEA, BIC or whatever)?

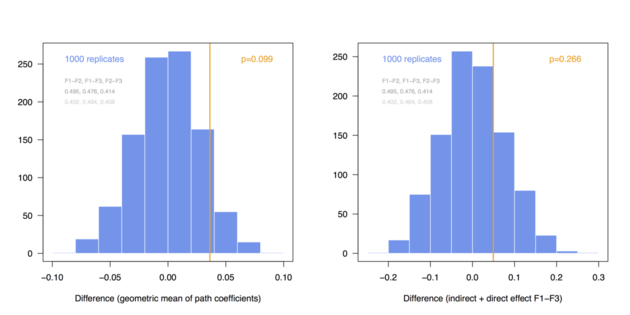
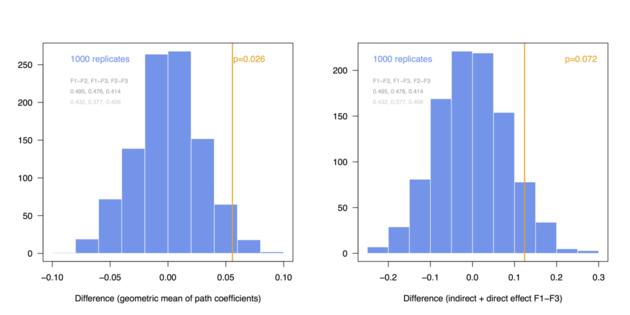
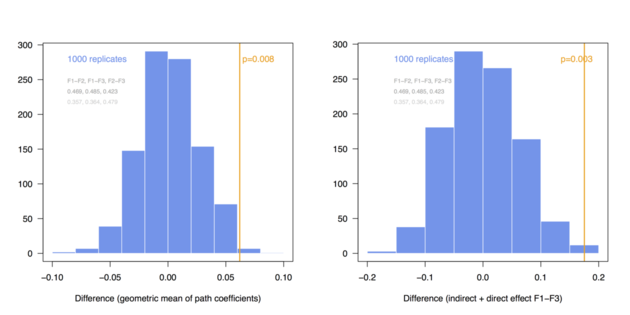
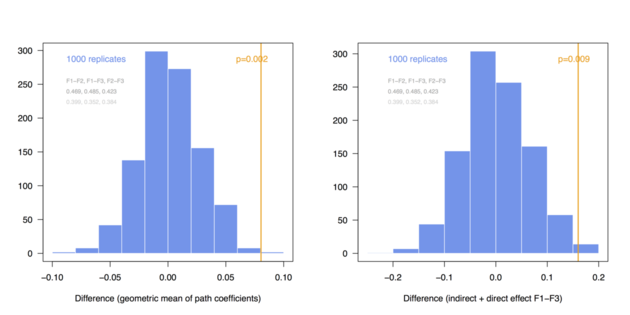
Here is a short illustration of permutation technique to assess the difference between two groups in terms of path coefficients estimated from PLS-PM. I am using the simsem package to generate artificial data according to a 3-factor model composed of a direct (F1-F3) and an indirect (F1-F2-F3) effect, with a pre-defined difference between two groups at the level of path coefficients (loadings, residuals errors and intercept/variance of the factors were constrained to be equal in the two groups). I will compute two summary measures, the difference between geometric mean¹ and between total effect of F1 onto F3 (b₁₃ + b₁₂ x b₂₃) in the two groups. The complete code is available as a Gist (it could certainly be optimized here and there, but I wrote this R script very quickly to illustrate those ideas).

Here are the distributions I got when considering a pre-defined difference of delta=0.03 (top) and 0.06 (bottom) between group-specific parameters (regression coefficients among endogenous variables, called BE in simsem::model()), for a fixed sample size of n=200 (these values can be changed at the top of the R script):

And here are the same results in the case of N = 300:

The above simulations just confirm that with a larger sample size we are more likely to demonstrate significant difference in multi-group comparison, especially when effect size increases. However, the main point is that it is quite easy to implement permutation- or bootstrap-based procedures to compare combination of parameter estimates between several groups.

The same resampling strategy could be applied to estimate number of subjects needed to reach a certain statistical power, but in fact the simsem package does that particularly well.