Petite note de synthèse rédigée à l’attention de mon fils pour son grand oral du BAC.

Le paradoxe des anniversaires, qui n’en est pas vraiment un, s’intéresse à la probabilité que deux personnes soient nées le même jour, plus précisément au nombre de personnes que l’on doit interroger avant que la probabilité de rencontrer deux personnes nées le même jour soit supérieure ou égale à 50 %.

Les hypothèses que l’on fera sont les suivantes : l’année comporte 365 jours et on néglige les années bisextiles.

On notera $p(n)$ la probabilité que au moins deux personnes prises parmi $n$ soient nées le même jour, et $n(p)$ le nombre de personnes nécessaires pour obtenir une probabilité $p$ donnée.

Le paradoxe vient du fait que les gens s’imaginent que la probabilité recherchée porte sur l’événement “deux personnes sont nées un même jour donné”, comme dans la question “quelle est la probabilté que le jour du grand oral de maths tombe le jour de mon anniversaire, en supposant que celui-ci puisse être organisé n’importe quel jour de l’année”. On va considérer le complémentaire de cette probabilité, ce qui nous évite d’énumérer tous les cas, et le soustraire de 1, et on dénotera $n$ le nombre de personnes attendues. On cherche donc $n$ tel que :

$$ 1-\left(\frac{364}{365}\right)^n = \frac{1}{2}. $$

La résolution de cette équation montre que si $n=253$, alors la probabilité recherchée est $> 1/2$. Qu’en est-il s’il l’on ne considère pas de date d’anniversaire fixe dans l’année ? C’est le problème énoncé plus haut.

Le plus simple est encore une fois de passer par le complémentaire en se demandant quelle est la probabilité que toutes les personnes interrogées ait un jour d’anniversaire différent.¹ Par dénombrement, on constate que le nombre de cas où $n$ personnes ont des anniversaires différents équivaut à un arrangement de $n$ objets pris parmi 365, soit $\frac{365!}{(365-n)!}$. Pour chaque personne il y a 365 possibilités de jour d’anniversaire, et donc comme il y a $n$ personnes il y a au total $365^n$ choix possibles. Le nombre de cas où $n$ personnes ont des anniversaires différents divisé par le nombre de possibilités donne donc la probabilité que tout le monde soit né un jour différent. Le complémentaire de cette probabilité équivaut à la probabilité de l’événement “au moins deux personnes sont nées le même jour”, soit :

$$ p(n) = 1 - \frac{365!}{(365-n)!} \cdot \frac{1}{365^n}. $$

 In[2]= N[1 - 365! / ((365-23)!365^23)]
out[2]= 0.507297

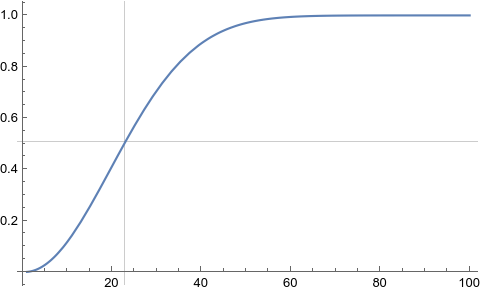
 In[3] = p[k_] := 1 - 365! / ((365-k)!365^k);
         Plot[p[k], {k, 1, 100}, GridLines -> {{23}, {p[23]}}];
         Table[N[p[k]], {k, 22, 25}]
Out[3] = {0.475695,0.507297,0.538344,0.5687}
                   ^^^^^^^^

L’expression $p(n)$ ci-dessus peut être approximée par $1-e^{-\frac{n^2}{2|E|}}$. Cette approximation s’obtient par le développement limité de $e^x = 1 + x + \mathcal{o}(x)$ pour $x$ au voisinage de 0. Comme discuté sur Wikipédia, ceci donne une approximation du nombre de personnes nécessaires pour avoir une probabilité $p$ d’observer au moins deux personnes avec le même jour d’anniversaire :

$$ n(p) \approx \sqrt{2\cdot 365\;\text{ln}\left(\frac{1}{1-p}\right)}. $$

 In[4]= n[k_] := Sqrt[2 365 Log[1 / (1-k)]];
        Table[N[n[k]], {k, 0.4, 0.6, 0.1}]
Out[4]= {19.3107,22.4944,25.863}
                 ^^^^^^^

Il existe d’autres approximations, et également d’autres façon de poser le problème (p.ex., nombre moyen de personnes nécessaires pour observer une paire d’anniversaires identiques, en supposant un échantillonnage avec ou sans remise).

Le paradoxe des anniversaires trouve des applications dans divers domaines, puisqu’il suffit de remplacer le concept de jour d’anniversaire par n’importe quel élément pris dans un entier dénombrable, par exemple des mots de passe générés aléatoirement.