Here is a little fact about Fibonacci numbers and their relation to some power series.

Let us assume a fair coin is tossed independently until two consecutive heads are observed.¹ The number of trials required to observe two heads follows a negative binomial distribution. We have to wait longer to observe the two heads in immediate succession. Consider the sequence $HTTHTHH$ and let $X+2$ be the number of trials required. Then in this case $X=5$. If we note $p_n=\Pr(X=n)$, enumerating the possible outcomes in the first two or three cases yields $p_0=\tfrac{1}{4}$ and $p_1=\tfrac{1}{8}$. A recursion relation can be constructed for larger values of $n$:

$$ p_n = \frac{1}{2}p_{n-1} + \frac{1}{4}p_{n-2}. $$

Using Mathematica, it is easy to verify the first terms of this recurrence:

RecurrenceTable[{a[n] == 0.5 a[n - 1] + 0.25 a[n - 2], a[0] == 0.25,
  a[1] == 0.125}, a, {n, 50}]

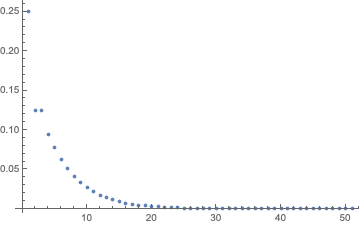
The corresponding probability generating function can also be obtained via GeneratingFunction. Note that it is also possible to use RSolve instead of RecurrenceTable, as shown in the following example where we generate the first terms of the Fibonacci sequence:

RecurrenceTable[{a[n] == a[n - 1] + a[n - 2], a[0] == 1,
  a[1] == 1}, a, {n, 10}]
RSolve[{a[n] == a[n - 1] + a[n - 2], a[0] == 1, a[1] == 1}, a[n], n]
Table[a[n] /. First[%], {n, 10}]

Or, equivalently:

GeneratingFunction[
  RSolve[{a[n] == a[n - 1] + a[n - 2], a[0] == 1, a[1] == 1}, a[n],
   n], n, x] // FullSimplify

The generating function is $\frac{1}{1-x (x+1)}$ in this case.

Back to our initial power series. for which the PGF reads:

$$ \frac{1}{4} + \frac{1}{8}\theta + \frac{1}{8}\theta^2 + \frac{3}{32}\theta^3 + \frac{5}{64}\theta^4 + \mathcal{O}(\theta^5). $$

Upon inspection of the above expression, we have $p_n = 2^{-(n+2)}F_{n+1}$, where $F_k$ is the $k$-th Fibonacci number. Note that the PGF of the reciprocal of this serie is $4-2\theta-\theta^2+\mathcal{O}(\theta^5)$, hence the PGF of $X$ can be written as:

$$ A(\theta) = \mathbb{E}(\theta^X) = \frac{1}{4-2\theta-\theta^2}. $$

The more I read on discrete math and Euler problems, the more I find Fibonacci numbers hanging around all over the place