I am currently reading Introduction to bioinformatics algorithms, by Jones and Pevzner. It’s a nice textbook for biologists and computer scientists since it provides gentle primers for both domains. Each chapter ends up with a series of exercises, generally of moderate difficulty, that you can solve analytically or using a computer program. Here is one example of such problem, from Chapter 2:

There are $n$ bacteria and 1 virus in a Petri dish. Within the first minute, the virus kills one bacterium and produces another copy of itself, and all of the remaining bacteria reproduce, making 2 viruses and $2 \cdot (n − 1)$ bacteria. In the second minute, each of the viruses kills a bacterium and produces a new copy of itself (resulting in 4 viruses and $2(2(n − 1) − 2) = 4n − 8$ bacteria; again, the remaining bacteria reproduce. This process continues every minute. Will the viruses eventually kill all the bacteria? If so, design an algorithm that computes how many steps it will take. How does the running time of your algorithm depend on $n$?

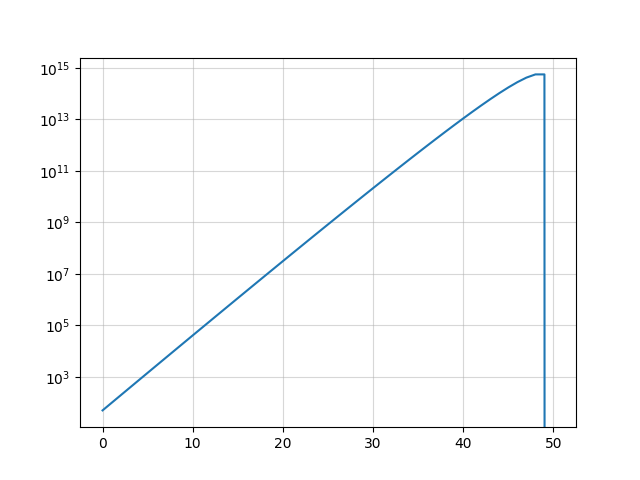
Let us write the recurrence relations describing how bacteria ($b$) and virus ($v$) populations evolve over time. At each epoch, each virus kill a bacterium and both samples double in number, which means $b(t) = 2 \cdot \big[ b(t-1) - v(t-1)\big]$ and $v(t) = 2 \cdot v(t-1)$. Henceforth, $b(t) = 2^t(n-t)$ and $v(t)=2^t$. Now, how many generations will it take for the viruses to kill all bacteria? Solving $b(t)=0$ yields $t=n$, suggesting that it will take exactly $n$ generations.

Now, what about writing this down in Python? This is just a simple loop ($\mathcal{O}(n)$), without regard to the inner numerical operations:

def evo(n, t):
    v = 2**t
    b = v * (n-t)
    if b < 0:
        return None
    return b

for t in range(100):
    pop = evo(50, t)
    if pop:
        print(t, pop)

As you can see, it will stop at $t=50$ and the numbers are growing very fast. The second to last step corresponds to the case where the number of virus is half that of bacteria: