Méthodes biostatistiques
ANOVA et comparaisons multiples

On utilise les données sur le polymorphisme du gène du récepteur estrogène, polymorphism.dta. Le chargement des données au format Stata nécessite le package foreign et peut être réalisé comme suit :

                        d <- foreign::read.dta("data/polymorphism.dta")
str(d)

'data.frame':   59 obs. of  3 variables:
 $ id      : num  1 2 3 4 5 6 7 8 9 10 ...
 $ age     : num  43 47 55 57 61 63 63 69 70 72 ...
 $ genotype: Factor w/ 3 levels "1.6/1.6","1.6/0.7",..: 1 1 1 1 1 1 1 1 1 1 ...
 - attr(*, "datalabel")= chr ""
 - attr(*, "time.stamp")= chr "16 Apr 2001 14:58"
 - attr(*, "formats")= chr [1:3] "%9.0g" "%9.0g" "%9.0g"
 - attr(*, "types")= int [1:3] 102 102 102
 - attr(*, "val.labels")= chr [1:3] "" "" "rflp"
 - attr(*, "var.labels")= chr [1:3] "ID Number" "Age at Diagnosis" "Genotype"
 - attr(*, "version")= int 7
 - attr(*, "label.table")=List of 1
  ..$ rflp: Named int [1:3] 1 2 3
  .. ..- attr(*, "names")= chr [1:3] "1.6/1.6" "1.6/0.7" "0.7/0.7"

Pour résumer la structure de données assez simple, on peut calculer l’âge moyen selon les groupes à l’aide de aggregate et représenter graphiquement les distributions conditionnelles de l’âge. Cela dit, le package Hmisc permet de calculer des résultats plus détaillés et plus facilement exploitables. On utilise la fonction, summary.formula, que l’on peut abréger à summary comme dans le cas du résumé d’un data frame ou d’une variable, et les mêmes arguments que dans le cas de aggregate.

                        summary(age ~ genotype, data = d, fun = smean.sd)

age     N= 59

+--------+-------+--+-------+-------+
|        |       | N|   Mean|     SD|
+--------+-------+--+-------+-------+
|genotype|1.6/1.6|14|64.6429|11.1811|
|        |1.6/0.7|29|64.3793|13.2595|
|        |0.7/0.7|16|50.3750|10.6388|
+--------+-------+--+-------+-------+
| Overall|       |59|60.6441|13.4943|
+--------+-------+--+-------+-------+

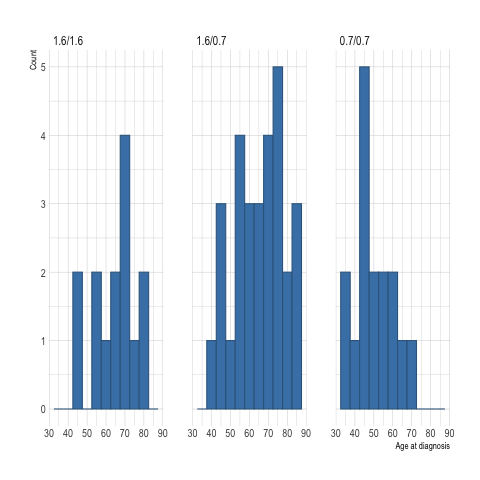
Pour représenter les distributions conditionnelles, il est possible d’utiliser des histogrammes d’effectif, des courbes de densité ou des boîtes à moustaches. Voici une solution avec des histogrammes à l’aide de ggplot2 :

                        p <- ggplot(data = d, aes(x = age)) +
  geom_histogram(binwidth = 5, fill = "steelblue", color = "steelblue4") +
  facet_wrap(~ genotype, ncol = 3) +
  labs(x = "Age at diagnosis", y = "Count")
p

La commande aov permet de décomposer la variance totale entre les différentes sources de variations (nécessairement de type factor) indiquées dans le modèle et le terme d’erreur ou “résiduelle”. On l’utilise généralement en combinaison avec summary.aov pour produire le tableau d’ANOVA :

                        m <- aov(age ~ genotype, data = d)
summary(m)

            Df Sum Sq Mean Sq F value  Pr(>F)
genotype     2   2316    1158    7.86 0.00098
Residuals   56   8246     147

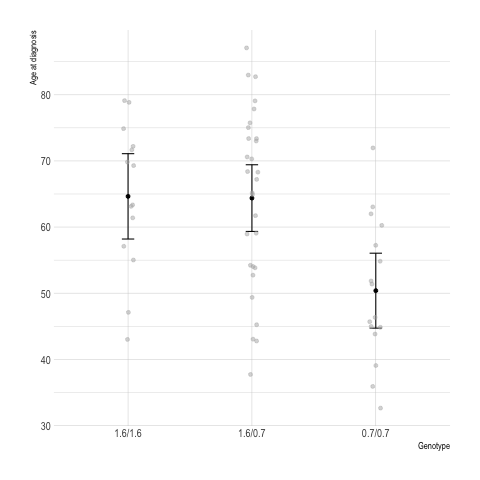
Une représentation graphique sous forme de moyennes conditionnelles s’obtient assez facilement avec ggplot2. Le calcul des moyennes et des intervalles de confiance à 95 % est réalisé avec Hmisc (attention, summarize n’accepte pas de notation par formule, contrairement à la fonction summary.formula du même package) :

                        r <- with(d, summarize(age, genotype, smean.cl.normal))
p <- ggplot(data = r, aes(x = genotype, y = age)) +
  geom_errorbar(aes(ymin = Lower, ymax = Upper), width=.1) +
  geom_point() +
  geom_jitter(data = d, width = .05, color = grey(.7), alpha = .5) +
  labs(x = "Genotype", y = "Age at diagnosis")
p

On peut comparer l’ensemble des paires de moyennes à l’aide de simples tests de Student non protégés :

                        with(d, pairwise.t.test(age, genotype, p.adj = "none"))

        Pairwise comparisons using t tests with pooled SD

data:  age and genotype

        1.6/1.6 1.6/0.7
1.6/0.7 0.947   -
0.7/0.7 0.002   5e-04

P value adjustment method: none

Notons que l’option par défaut retenue pour pairwise.t.test est de travailler avec la variance commune de l’ensemble des groupes, comme dans l’ANOVA. Pour retrouver les mêmes résultats avec la commande t.test, il faudra désactiver cette option :

                        with(d, pairwise.t.test(age, genotype, p.adj = "none", pool.sd = FALSE))
t.test(age ~ genotype, data = d, subset = genotype != "0.7/0.7", var.equal = TRUE)

        Pairwise comparisons using t tests with non-pooled SD

data:  age and genotype

        1.6/1.6 1.6/0.7
1.6/0.7 0.946   -
0.7/0.7 0.001   4e-04

P value adjustment method: none

        Two Sample t-test

data:  age by genotype
t = 0.06408, df = 41, p-value = 0.949
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -8.04237  8.56947
sample estimates:
mean in group 1.6/1.6 mean in group 1.6/0.7
              64.6429               64.3793

Les mêmes résultats peuvent se retrouver à partir du modèle linéaire directement. Encore une fois, il faut s’assurer que les variables catégorielles sont bien représentées comme des facteurs sous R :

                        m <- lm(age ~ genotype, data = d)
summary(m)

Call:
lm(formula = age ~ genotype, data = d)

Residuals:
    Min      1Q  Median      3Q     Max
-26.379  -8.643   0.625   8.621  22.621

Coefficients:
                Estimate Std. Error t value Pr(>|t|)
(Intercept)       64.643      3.243   19.93   <2e-16
genotype1.6/0.7   -0.264      3.949   -0.07   0.9470
genotype0.7/0.7  -14.268      4.441   -3.21   0.0022

Residual standard error: 12.1 on 56 degrees of freedom
Multiple R-squared:  0.219,     Adjusted R-squared:  0.191
F-statistic: 7.86 on 2 and 56 DF,  p-value: 0.000978

Le test d’ensemble pour le modèle indiqué au bas des résultats précédents correspond au test de Fisher-Snedecor de l’ANOVA. On peut également le retrouver en affichant le tableau d’ANOVA du modèle de régression à l’aide de anova :

anova(m)

Analysis of Variance Table

Response: age
          Df Sum Sq Mean Sq F value   Pr(>F)
genotype   2   2316  1157.9   7.863 0.000978
Residuals 56   8246   147.2

On utilise les données sur le gain de poids chez des rats soumis à différents régimes alimentaires, weight.rda. Le chargement des données est réalisé ci-dessous :

                        load("data/weight.rda")
str(weight)

'data.frame':   10 obs. of  4 variables:
 $ V1: int  90 76 90 64 86 51 72 90 95 78
 $ V2: int  73 102 118 104 81 107 100 87 117 111
 $ V3: int  107 95 97 80 98 74 74 67 89 58
 $ V4: int  98 74 56 111 95 88 82 77 86 92

Les variables peuvent être décrites par colonnes mais il est préférable de réarranger le tableau sous forme de data frame, afin d’avoir une seule variable statistique par colonne :

                        d <- data.frame(weight = as.numeric(unlist(weight)),
                type   = gl(2, 20, labels = c("Beef", "Cereal")),
                level  = gl(2, 10, labels = c("Low", "High")))
head(d)

  weight type level
1     90 Beef   Low
2     76 Beef   Low
3     90 Beef   Low
4     64 Beef   Low
5     86 Beef   Low
6     51 Beef   Low

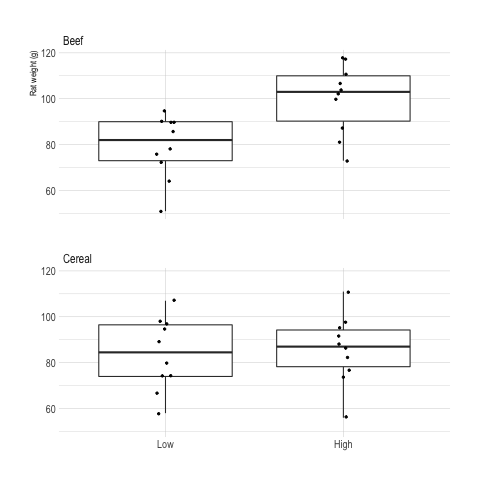
Voici un résumé graphique possible des données individuelles avec le package ggplot2 :

                        p <- ggplot(data = d, aes(x = level, y = weight)) +
  geom_boxplot(position = position_dodge()) +
  geom_jitter(size = .8, width = .05) +
  facet_wrap(~ type, nrow = 2) +
  labs(x = NULL, y = "Rat weight (g)")
p

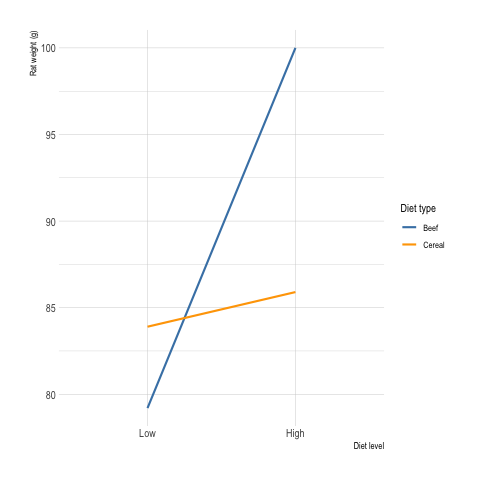
Pour visualiser l’interaction entre les deux variables, on peut utiliser un simple tracé de moyennes conditionnelles :

                        p <- ggplot(data = d, aes(x = level, y = weight, color = type)) +
  stat_summary(fun.y = mean, geom = "line", aes(group = type), size = 1) +
  scale_color_manual("Diet type", values = c("steelblue", "orange")) +
  labs(x = "Diet level", y = "Rat weight (g)")
p

Une autre manière de procéder consisterait à travailler avec le data frame de données agrégées, r, et utiliser geom_line au lieu de stat_summary, toujours en veillant à ajouter une esthétique de groupement. La fonction geom_errorbar permet de rajouter aisément des barres d’erreur (écart-type, erreur-type ou intervalles de confiance – à calculer séparément), comme on l’a vu plus haut. Les statistiques nécessaires peuvent être calculées avec les packages plyr, dplyr ou Hmisc comme proposé plus haut. Voici un exemple avec des intervalles de confiance à 95 % :

                        with(d, summarize(weight, llist(type, level), smean.cl.normal))

    type level weight   Lower    Upper
2   Beef   Low   79.2 69.2660  89.1340
1   Beef  High  100.0 89.1721 110.8279
4 Cereal   Low   83.9 72.6626  95.1374
3 Cereal  High   85.9 75.1540  96.6460

Le package Hmisc propose aussi des fonctions graphiques pour représenter, entre autres, les effets d’interaction.

Le modèle d’ANOVA à deux facteurs avec interaction s’écrit :

                        m1 <- aov(weight ~ type * level, data = d)
summary(m1)

            Df Sum Sq Mean Sq F value Pr(>F)
type         1    221     221    0.99  0.327
level        1   1300    1300    5.81  0.021
type:level   1    884     884    3.95  0.054
Residuals   36   8049     224

La notation type * level est équivalente à type + level + type:level, où type:level désigne l’interaction entre les facteurs type et level. Ce terme d’interaction n’étant pas significatif, il est possible de proposer un modèle plus simple :

                        m0 <- aov(weight ~ type + level, data = d)
summary(m0)

            Df Sum Sq Mean Sq F value Pr(>F)
type         1    221     221    0.91  0.345
level        1   1300    1300    5.38  0.026
Residuals   37   8933     241

On retrouvera le test de l’interaction en comparant ces deux modèles emboîtés, m0 et m1, à l’aide de anova (dans le cas gaussien, ce sont des statistiques F qui sont calculées) :

anova(m0, m1)

Analysis of Variance Table

Model 1: weight ~ type
level
Model 2: weight ~ type * level
  Res.Df  RSS Df Sum of Sq     F Pr(>F)
1     37 8933
2     36 8049  1     883.6 3.952 0.0545

Puisque la variable level possède deux niveaux, il est également possible de retrouver à peu près les mêmes résultats que ceux du tableau d’ANOVA à l’aide d’un test de Student puisque l’effet de ce facteur est supposé être indépendant de l’autre terme inclus dans le modèle :

                        r <- t.test(weight ~ level, data = d, var.equal = TRUE)
r
r$statistic^2

        Two Sample t-test

data:  weight by level
t = -2.323, df = 38, p-value = 0.0256
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -21.33588  -1.46412
sample estimates:
 mean in group Low mean in group High
             81.55              92.95

      t
5.39495

La fonction pairwise.t.test est limitée au cas à un facteur. On peut néanmoins reconstruire le terme d’interaction à l’aide de interaction, ce qui nous fournira un facteur codant les groupes issus du croisement de l’ensemble des niveaux des deux facteurs, encore appelé traitements. Cette technqiue permet également de réaliser un test d’égalité des variances ou de visualiser la distribution entre traitements pour vérifier les conditions de validité du modèle.

Voici un exemple de tests de Student avec correction de Bonferroni :

                        with(d, pairwise.t.test(weight, interaction(type, level), p.adj = "bonf"))

        Pairwise comparisons using t tests with pooled SD

data:  weight and interaction(type, level)

            Beef.Low Cereal.Low Beef.High
Cereal.Low  1.00     -          -
Beef.High   0.02     0.13       -
Cereal.High 1.00     1.00       0.25

P value adjustment method: bonferroni

Et voici pour la distribution du poids des rats entre traitements :

                        p <- ggplot(data = d, aes(x = interaction(type, level, sep = "/"), y = weight)) +
  geom_boxplot() +
  labs(x = "Treatment (Diet type x Diet level)", y = "Rat weight (g)")
p

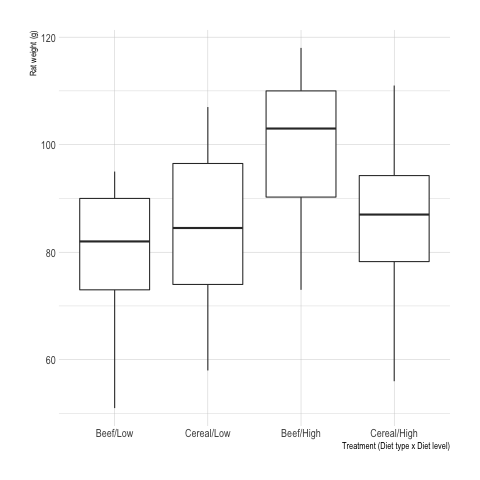
L’alternative consiste à utiliser des tests post-hoc de type Tukey HSD à l’aide de TukeyHSD, ou de l’alternative disponible via la fonction multcomp::glht(). Voici une illustration avec le package multcomp, plus flexible et plus générale que la fonction de base de R. À noter qu’il est également nécessaire de travailler avec le terme d’interaction et d’utiliser lm au lieu de aov :

                        d$tx <- with(d, interaction(type, level))
m <- lm(weight ~ tx, data = d)
r <- glht(m, linfct = mcp(tx = "Tukey"))
summary(r)

         Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: Tukey Contrasts


Fit: lm(formula = weight ~ tx, data = d)

Linear Hypotheses:
                              Estimate Std. Error t value Pr(>|t|)
Cereal.Low - Beef.Low == 0        4.70       6.69    0.70    0.895
Beef.High - Beef.Low == 0        20.80       6.69    3.11    0.018
Cereal.High - Beef.Low == 0       6.70       6.69    1.00    0.749
Beef.High - Cereal.Low == 0      16.10       6.69    2.41    0.094
Cereal.High - Cereal.Low == 0     2.00       6.69    0.30    0.991
Cereal.High - Beef.High == 0    -14.10       6.69   -2.11    0.170
(Adjusted p values reported -- single-step method)

Ces résultats vont dans le même sens que ce que suggère le résultat non significatif pour le test de l’interaction (cf. les deux comparaisons extrêmes Cereal.Low - Beef.Low et Cereal.High - Beef.High).

Attention au codage de de la variable dose.

1. Réaliser une ANOVA à deux facteurs pour répondre aux questions suivantes : (a) existe t-il un effet du mode d’administration de la vitamine C (supp) sur la longueur des odontoblastes, et (b) cet effet est-il dépendant du dosage journalier ?
2. L’effet dose est-il linéaire ? Vérifier la linéarité de la relation len ~ dose en utilisant (a) une approche de régression et (b) une approche par ANOVA avec des contrastes polynomiaux.

On souhaite comparer l’ensemble des paires de moyennes pour le croisement des deux variables supp et dose.

1. Indiquer les résultats obtenus avec une approche par tests de Student sans correction pour les tests multiples.
2. Idem mais en contrôlant pour le risque d’expérience global (FWER) par (a) une technique d’ensemble (Bonferroni ou Sidák) et (b) une technique par étape (Holm). Les conclusions diffèrent-elles ?

On souhaite comparer des groupes spécifiques d’observations.

1. On s’intéresse à la comparaison des données moyennes dans le groupe OJ pour les doses 0.5 et 1 mg réunies avec les données moyennes dans le groupe VC pour les mêmes doses. Réaliser le test correspondant.
2. On s’intéresse à la comparaison des données moyennes dans le groupe OJ pour les doses 0.5 et 1 mg réunies avec les données moyennes dans le groupe OJ pour la dose 2 mg. Réaliser le test correspondant.
3. On s’intéresse à la comparaison des données moyennes dans le groupe OJ pour les doses 0.5 et 1 mg réunies avec les données moyennes dans le groupe VC pour les doses 1 et 2 mg. Réaliser le test correspondant.

R utilise des sommes de carré de type I, encore appelées séquentielles. Dans le cas où les effectifs sont balancés entre les traitements, on obtiendra les mêmes résultats quelle que soit l’approche utilisée. En cas de déséquilibre d’effectifs, en revanche, ce n’est plus le cas et certains auteurs recommendent d’utiliser des sommes de carré de type III, voire de type II. Comparer les résultats obtenus en utilisant ces trois types de sommes de carré, obtenus à l’aide des fonctions add11 ou drop1 et Anova du package car pour le modèle à deux facteurs sur les données ToothGrowth. Le déséquilibre d’effectifs pourra être imposé par une suppression aléatoire de 10 % des observations.

set.seed(101)
ToothGrowth[sample(1:nrow(ToothGrowth), 6),"len"] <- NA