Yesterday I worked on an interesting problem in Python. Given a set of (x,y) points in a plane, I needed to compute the area of the whole cloud of points. An easy solution would be to compute the convex hull of the 2D points, but of course it would overestimate the total area in the presence of strong outlying values at the periphery. We could rely on Delaunay triangulation for that purpose, or maybe its dual (the Voronoi diagram) to minimize the overestimation, as shown in the Figure below (left panel). Another approach would consist in summing of the areas of all interior polygons, which is the same as the sum of the polygon areas defined by the Delaunay triangulation minus the exterior polygons, i.e., those not surrounded entirely by other polygons.

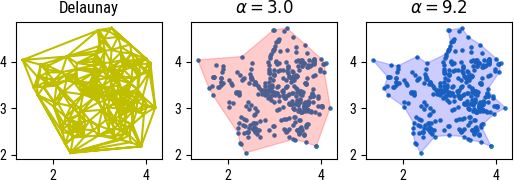
Luckily, I found a nice package on Pypi that handles all that stuff right.¹ Note that there’s a close relationship between alpha shape and Delaunay triangulation: As described on Wikipedia, each edge or triangle of the Delaunay triangulation may be associated with a characteristic radius, the radius of the smallest empty circle containing the edge or triangle. Furthermore, when $\alpha=0$, we get the classical convex hull. See also Introduction to Alpha Shapes (PDF).

Intuitively an alpha shape can be conceptualized as follows. Imagine carving out the plane using a cookie scoop of radius 1/α, without removing any of the points in the point cloud. The shape that remains is the shape of the point cloud. If we replace the arc-like edges, due to the circular rim of the scoop, with straight segments, we are left with the alpha shape of parameter α.

It even features an optimize utility that allows to find the best thresholding parameter value, which relies on brute force search. In the above figure, the middle and right panels show the result of using an arbitrary α value versus the optimized one. And since it internally relies on Python’s shapely Polygon objects, you’ll get the area of the alpha shape for free.