Again, looking at the MedStats mailing-list I found an interesting discussion on how to Define significant changes in neuropsychological tests. The article that serves as a basic reference for this discussion is:

Raymon, P.D., Hinton-Bayre, A.D., Radel, M., Ray, M.J., and Marsh, N.A. (2006). Assessment of statistical change criteria used to define significant change in neuropsychological test performance following cardiac surgery. European Journal of Cardio-thoracic Surgery, 29: 82-88.

Objective: This paper compares four techniques used to assess change in neuropsychological test scores before and after coronary artery by pass graft surgery (CABG), and includes a rationale for the classification of a patient as overall impaired. Methods: A total of 55 patients were tested before and after surgery on the MicroCog neuropsychological test battery. A matched control group underwent the same testing regime to generate test—retest reliabilities and practice effects. Two techniques designed to assess statistical change were used: the Reliable Change Index (RCI), modified for practice, and the Standardised Regression-based (SRB) technique. These were compared against two fixed cutoff techniques (standard deviation and 20% change methods). Results: The incidence of decline across test scores varied markedly depending on which technique was used to describe change. The SRB method identified more patients as declined on most measures. In comparison, the two fixed cutoff techniques displayed relatively reduced sensitivity in the detection of change. Conclusions: Overall change in an individual can be described provided the investigators choose a rational cutoff based on likely spread of scores due to chance. A cutoff value of ≥ 20% of test scores used provided acceptable probability based on the number of tests commonly encountered. Investigators must also choose a test battery that minimizes shared variance among test scores.

Hereby, I do a rather quick search on Google and get the following articles compiled in a BibTeX file: RCSC.html or RCSC.bib. Note that I’ve bookmarked most of them on my del.icio.us account. A rather interesting entry was found to be the website of Chris Evans who wrote some notes on this topic. A somewhat good summary is available in PDF: Jacobson and Truax (1991), Clinical significance: a statistical approach to defining meaningful change in psychotherapy research.

Following Bain & Dollaghan,⁽¹⁾ a clinically significant change is a change in client performance that (1) can be shown to result from treatment rather than from maturation or other uncontrolled factors, (2) can be shown to be real rather than random, and (3) can be shown to be important rather than trivial. There is also an interesting overview of statistical significance compared to clinical significance and an article wrote by Christensen and published in Prevention & Treatment which is available on-line: The Clinical Significance of Neil’s Couple Therapy Research.

Basically, a reliable change is defined with respect to the reliability of the measurement instrument used to evaluate the patient. Obviously, the reliability of a given instrument (questionnaire, inventory, etc.) can be estimated in many ways which leads to the distinction between structural consistency, internal consistency or temporal consistency. The latter, often called test-retest reliability, may be obtained using a simple intra-class correlation. The interested reader is referred to Thompson’s textbook⁽³⁾ to fully appreciate the interest of reliability assessment.

C. Evans gives the following formula to estimate a criterion level that would indicate change occurring less than 5% of the time just due to measurement error:

$$ \sigma_1\times\sqrt{2}\times\sqrt{1-\Phi}, $$

where $\Phi$ stands for the reliability coefficient. This formula originates from Christensen and Mendoza,⁽⁴⁾ after correcting for the fact we are looking at difference between two unreliable measurements (hence the square root of 2 used in the above formula).

Note that Evans also recommends using Cronbach α, from the observed data or a previous study, as an estimate of the measurement reliability. Although there is a long-standing debate about the difference between internal vs. temporal (scores) consistency (see, e.g. Thompson⁽³⁾), the use of an α gathered through previous data is not the best way to ascertain present scores reliability. Indeed, reliability is a property of scores, not of the instrument itself. Thus, one would get different reliability estimates when using different data from the same measurement device!

This formula can be implemented without effort in R. For instance, 

rc.crit <- function(s,rel,conf.level=.05) { 
  qnorm(1-conf.level/2)*s*sqrt(2)*sqrt(1-rel) 
}

Varying the SD or the reliability leads to the following expectations

xx <- expand.grid(s = seq(.5,3.5,by=.5), rel = seq(.5,.95,by=.05))
yy <- rc.crit(xx[,1],xx[,2])
library(lattice)
contourplot(yy ~ xx$s + xx$rel, region=TRUE, cuts=20)

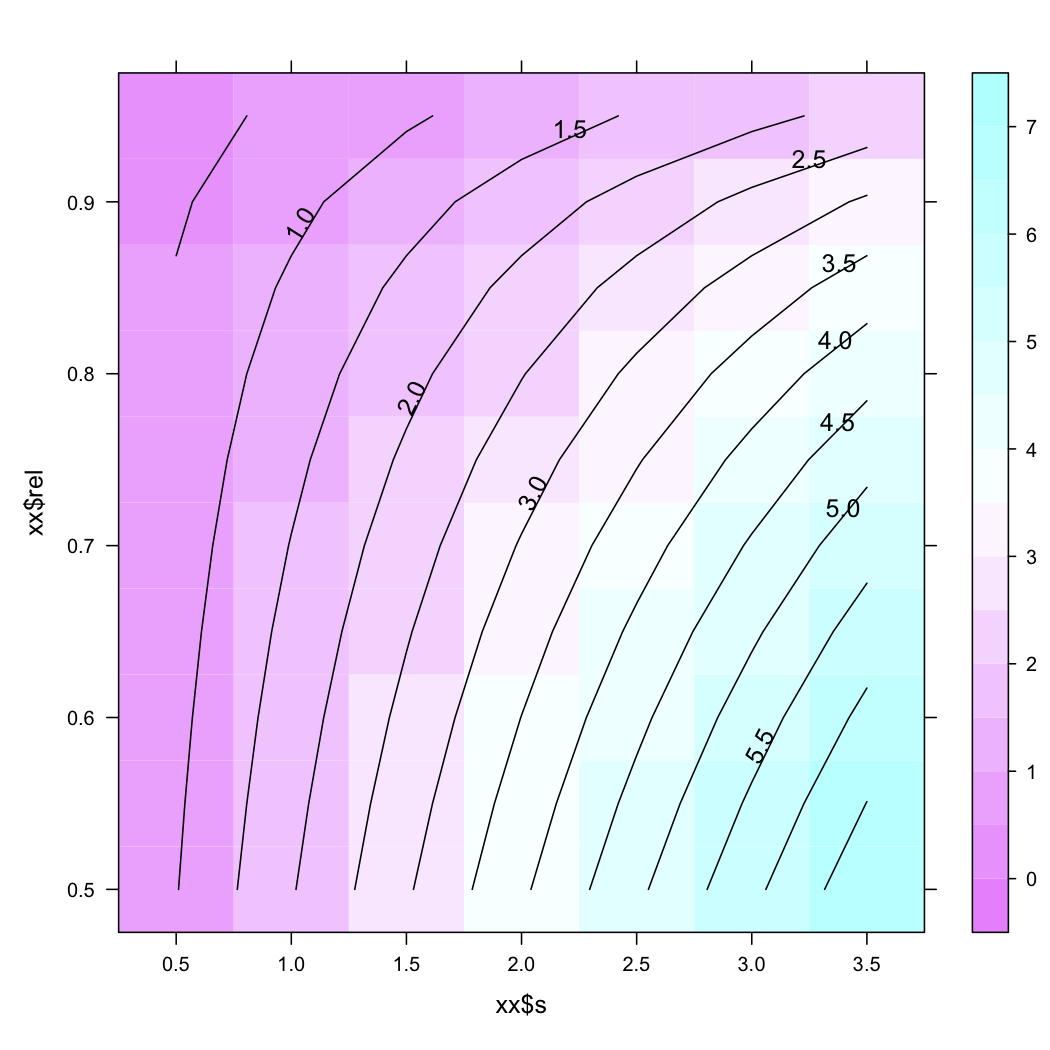
Now, a clinical significant change is not defined as a change greater than what might be expected by measurement error but it is viewed as a change of the patient’s location with respect to normative or population-based criterion,⁽⁵⁾ e.g., its location from the mean ± 2 SD.

Other methods include, e.g., standardized regression-based technique. Analysis of covariance might also be useful when one wants to compare a simple change at one period. Using the baseline (T0) as a covariate, we may test for difference between two groups or set of observations. Obviously, this relies on the assumption that the two groups are comparable in their means at the baseline. Another solution is to resort to Latent Growth Modeling (LGM, but one also talks of Latent Trajectories). In this case, we are not only modeling the change (max - min) but we are tackling the process of change directly. LGM is a longitudinal analysis technique to estimate growth over a period of time. For a detailed explanation of such technique, please refer to Acock⁽⁹⁾ or this webpage which summarizes a number of significant contributions to this field, or the supplemental Chapter D of Kline’s book, Principles and Practice of Structural Equation Modeling (1998): Latent Growth Models. This model-based approach allows to model constant, linear, accelerating or decreasing change, and this trajectory can be compared to controls trajectory. Note, however, that this requires a comfortable sample size, as many latent variable models.

References

1. Bain, B.A. and Dollaghan, C.A. (1991). The Notion of Clinically Significant Change. Language, Speech, and Hearing Services in Schools, 22, 264—270.
2. Hsu, L.M. (1989). Random Sampling, Randomization, and Equivalence of Contrasted Groups in Psychotherapy Outcome Research. Journal of Consulting and Clinical Psychology, 57(1), 131—137.
3. Thompson, B. (2003). Score Reliability, Contemporary Thinking on Reliability Issues. Sage Publications.
4. Christensen, L. and Mendoza, J.L. (1986). A method of assessing change in a single subject: an alteration of the RC index. Behavior Therapy, 17, 305—308.
5. Jacobson, N.S., Follette, W.C., and Revenstorf, D. (1984). Psychotherapy outcome research: Methods for reporting variability and evaluating clinical significance. Behavior Therapy, 15, 336—352.
6. Tombaugh, T.N. (2005). Test-retest reliable coefficients and 5-year change scores for the MMSE and 3MS. Archives of Clinical Neuropsychology, 4(20), 485—583.
7. Maassen, G.H. (2004). The standard error in the Jacobson and Truax Reliable Change Index: The classical approach to the assessment of reliable change. Journal of the International Neuropsychological Society, 10, 888—893.
8. Maassen, G.H. (2000). Kelley’s formula as a basis for the assessment of reliable change. Psychometrika, 65(2), 187—197.
9. Acock, A.C.  Latent Growth Curve Analysis: A Gentle Introduction.
10. Rabe-Hesketh, S. and Skrondal, A. (2005).  Multilevel Latent Growth Modeling With Latent-Trait-Dependent Dropout: A Cluster Randomized Sex Education Intervention.
11. Park, I. and Schutz, R.W. (2005). An introduction to latent growth models: analysis of repeated measures physical performance data. Research Quarterly for Exercise and Sport, 76(2), 176—192.